In the question number 35, the acceleration of the particle at $t = 1$ is

A

$2 ˆ j m s^{- 2}$

B

$- 2 ˆ j m s^{- 2}$

C

$4 ˆ j m s^{- 2}$

D

$- 4 ˆ j m s^{- 2}$

Text Solution

Verified by Experts

The correct Answer is:C

From the previous question, $\to v = 3 ˆ i + 4 t ˆ j m s^{- 1}$
$∴$ Acceleration, $\to a = \frac{d \to v}{d t} = 4 ˆ j m s^{- 2}$
Acceleration of the particle remains constant at all times.

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - HOTS
6videos
MOTION IN A PLANE
BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - EXEMPLER PROBLEMS
9videos
MOTION IN A PLANE
BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15videos
MECHANICAL PROPERTIES OF SOLIDS
BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6videos
MOTION IN A STRAIGHT LINE

Similar Questions

Knowledge Check

Question 1 - Select One
For the previous question, the acceleration of the particle at any time $t$ is :
A $- 0.8 m / s^{2}$
B $0.8 m / s^{2}$
C $- 0.6 m / s^{2}$
D $0.5 m / s^{2}$
Question 2 - Select One
For the previous question, the acceleration of the particle at any time $t$ is $:$
A $- 0.8 m / s^{2}$
B $0.8 m / s^{2}$
C $- 0.6 m / s^{2}$
D $0.5 m / s^{2}$
Question 3 - Select One
The velocity -time $(v - t)$ graph of a particle moving in a straight line is shown in figure. The acceleration of the particle at $t = 9$ is:

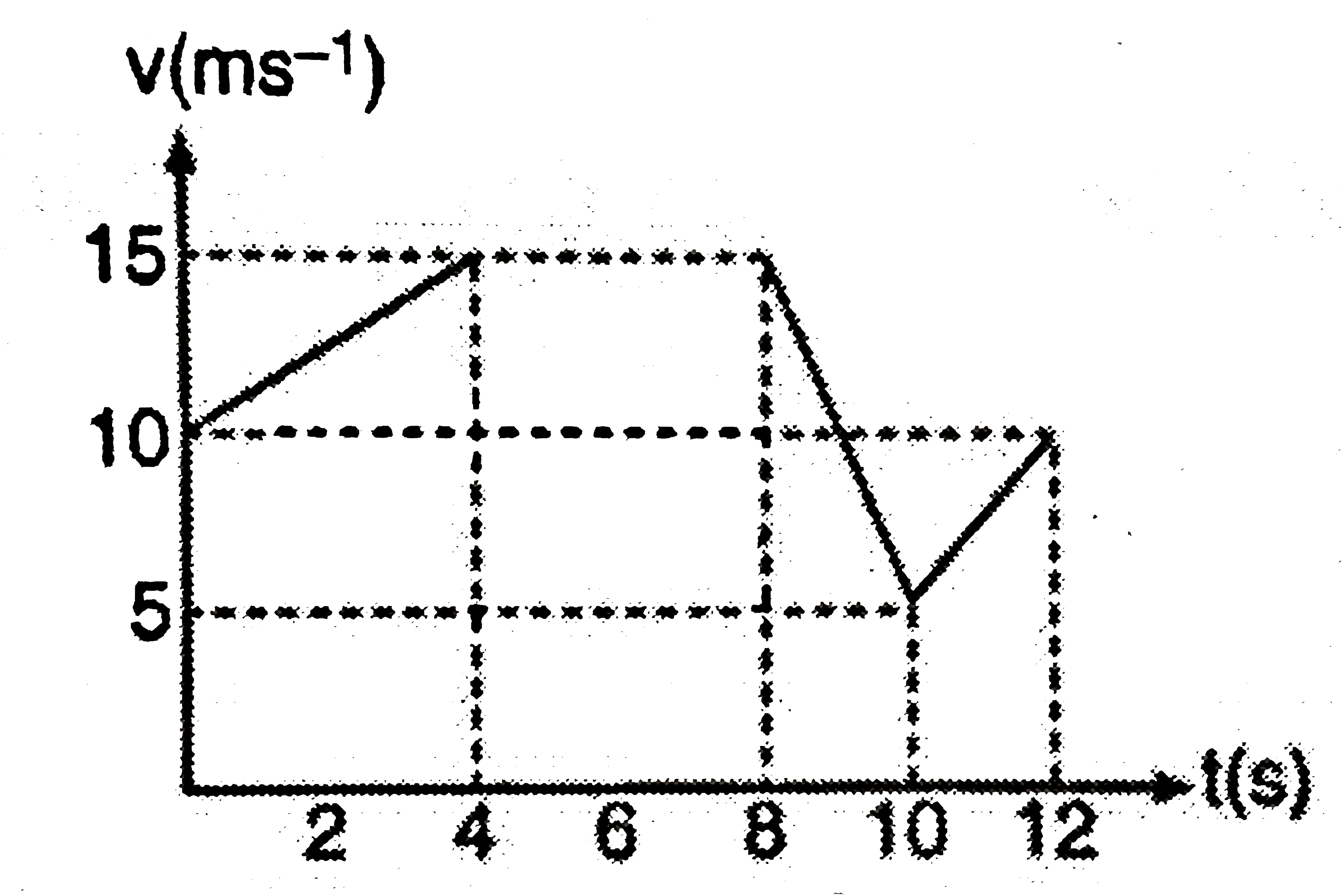Azero
B $5 m s^{- 2}$
C $- 5 m s^{2}$
D $- 2 m s^{- 2}$

NCERT FINGERTPS ENGLISH-MOTION IN A PLANE -Assertion And Reason

Home
Ask Doubt
Profile