In Fig. shown, the rod has a resistance R, the horizontal rails have negligible friction. A battery of emf E and negligible internal resistance is connected between points aandb. The rod is released from rest.

The current when the rod attains its terminal speed is
(a) 2ER
(b) zero if both wires slide in opposite directions
(c ) 22ER
(d) E2R
The correct Answer is:B
(b)Due to applied emf, current will flow as shown. Due to this current and magnetic field B, force on the wire will act towards right and rod will start moving towards right. Let at any instant, its velocity, emf e=Blv will be induced as shown.

Net emf: E−Blv,I=E−BlvR ....(i)
F=IBl=(E−BlvR)Bl ...(ii)
→ mdvdt=(E−Blv)BlR
mRBldvdt=E−Blv → int_(0)^(v)(dv)/(E - Blv) = int_(0)^(t)(Bl)/(mR)dt<br>rarr[(1n(E - Blv))/(-Bl)]_(0)^(v) = (Bl)/(mR)trarr1n((E - Blv)/(E)) = (-B^(2)l^(2))/(mR)t<br>rarr(E - Blv)/(E) = e^(t//tau) → v = (E)/(Bl)[1 - e^(t//tau)]<br>Velocitywill∈creaseup→t oo,andt=∞, velocity will be maximum and constant.
Also, when the velocity is constant, net force on the rod will become zero, so putting F=0 in equation (ii), we get
vterminal=EBl
hen the rod attains terminal velocity, then from equation (i), I=0.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:CENGAGE PHYSICS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercises Integer
Explore 9 Videos
- ELECTROMAGNETIC INDUCTIONBook:CENGAGE PHYSICS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Archives Fill In The Blanks
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:CENGAGE PHYSICS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercises Asserton - Reasoning
Explore 8 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSExercise:dpp 3.3
Explore 15 Videos
Similar Questions
In Fig. shown, the rod has a resistance R, the horizontal rails have negligible friction. A battery of emf E and negligible internal resistance is connected between points aandb. The rod is released from rest.

The velocity of the rod as function of time is
View SolutionIn Fig. shown, the rod has a resistance R, the horizontal rails have negligible friction. A battery of emf E and negligible internal resistance is connected between points aandb. The rod is released from rest.

after some time, the rod will approach a terminal speed . Find an expression for it.
View SolutionA 3 volt battery with negligible internal resistance is connected in a circuit as shown in the figure. The current I, in the circuit will be

View SolutionA series combination of L and R is connected to a battery of emf E having negligible internal resistance. The final value of current depends upon
View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

View SolutionA solenoid of resistance R and inductance L has a piece of soft iron inside it. A battery of emf E and of negligible internal resistance is connected across the solenoid as shown in Fig. At any instant, the piece of soft iron is pulled out suddenly so that inductance of the solenoid decrease to ηL(η<1) with battery remaining connected.
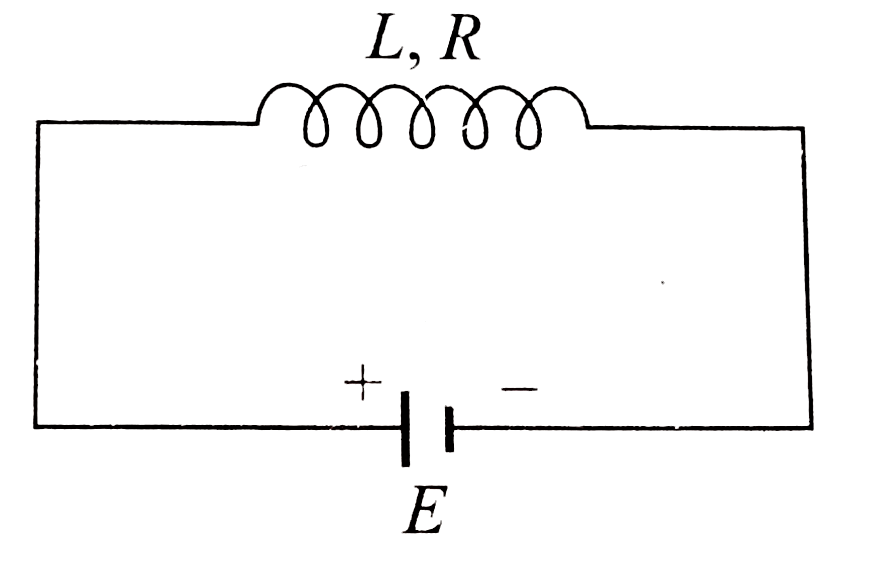
Assume t = 0 is the instant when iron piece has been pulled out, the current as a function of time after this is
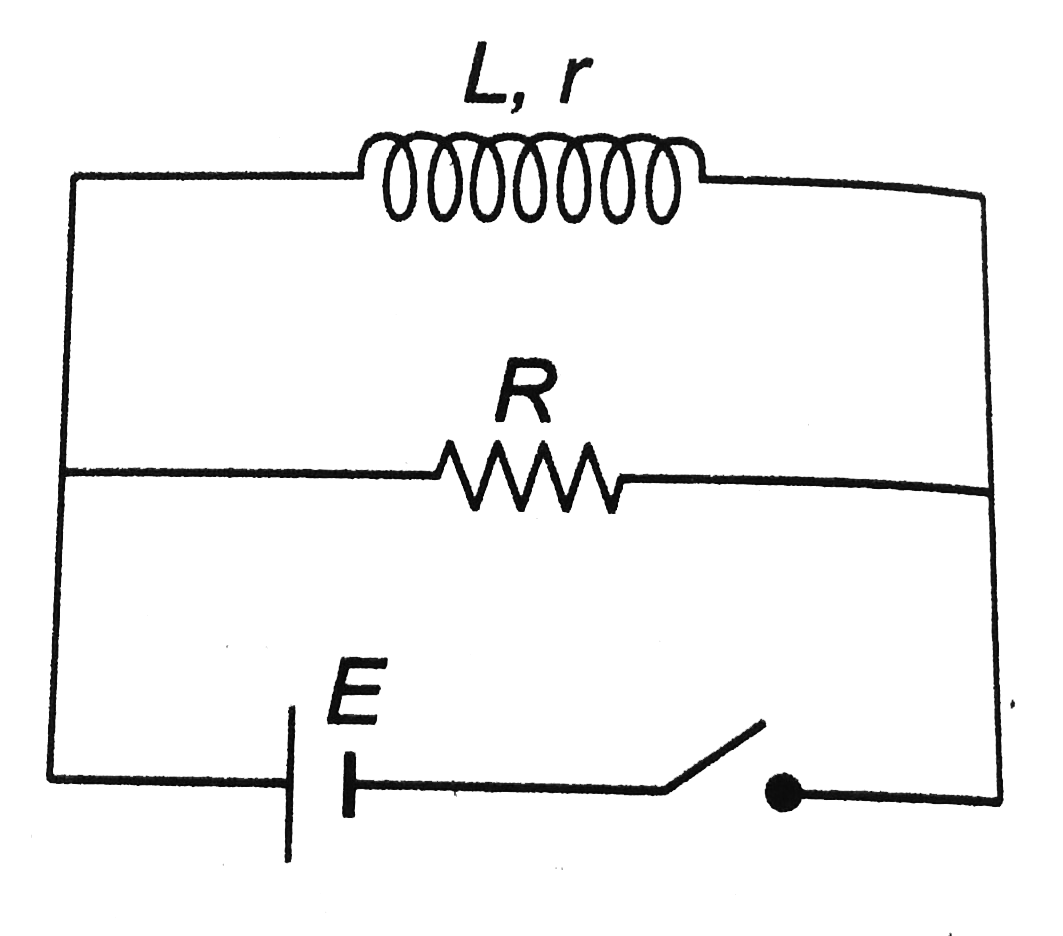
View SolutionA solenoid of inductance L with resistance r is connected in parallel to a resistance R. A battery of emf E and of negligible internal resistance is connected across the parallel combination as shown in the figure. At time t=0, switch S is opened, calculate
(a) current through the solenoid after the switch is opened.
(b) amount of heat generated in the solenoid.
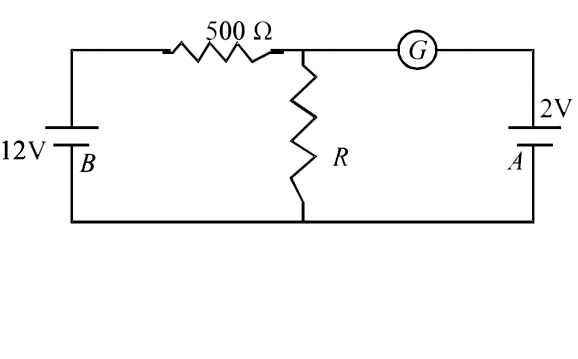
View SolutionIn the circuit, the galvanometer G shows zero deflection. If the batteries A and b have negligible internal resistance, the value of the resistor R will be -
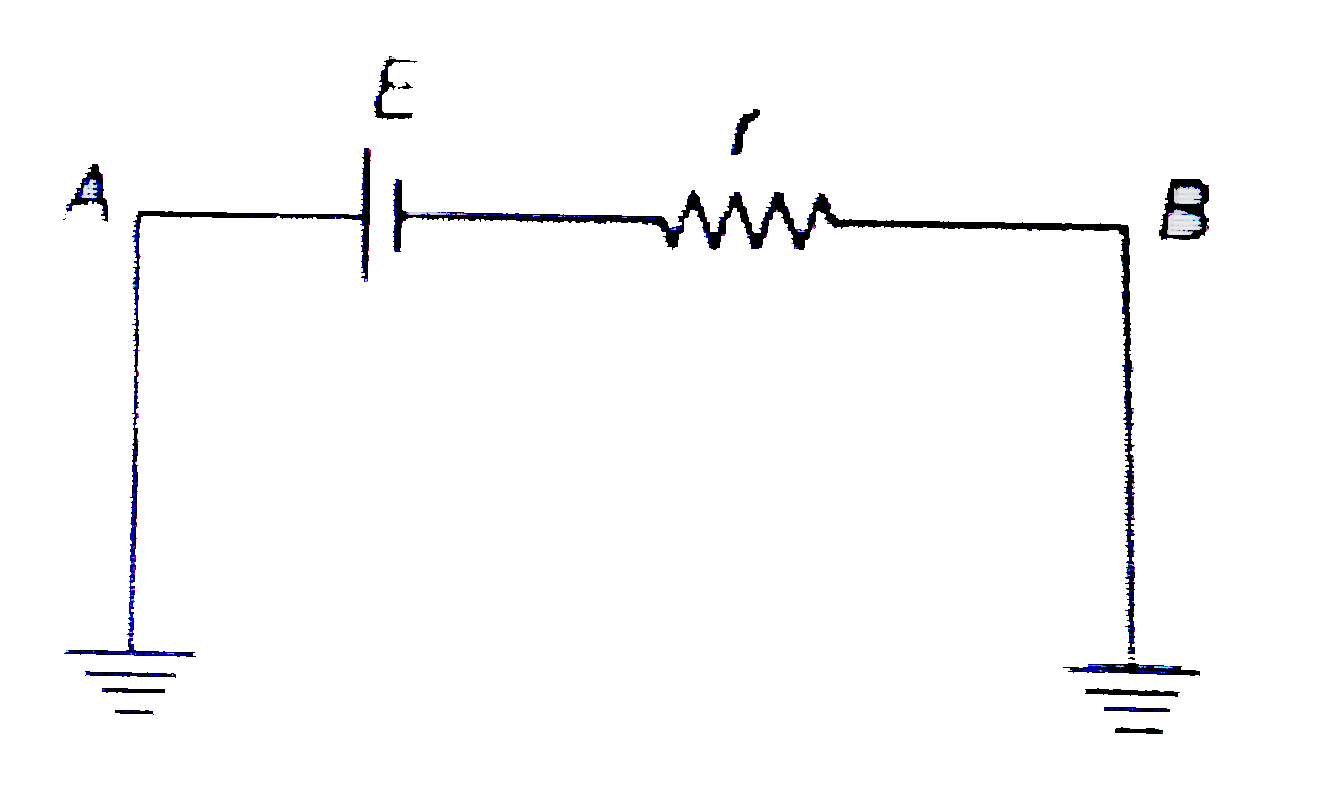
View SolutionBoth terminals of a battery of emf E and internal resistance r are grounded as shown. Select the correct alternative(s).
View Solution(a) Three resistors 2Ω,4Ωand5Ω are combined in parallel. What is the total resistance of the combination ?
(b) If the combination is connected to a battery of emf 20 V and negligible internal resistance, determine the current through each resistor, and the total current drawn from the battery.
View Solution

