Consider a uniform rod of mass M and length L is hinged at one end as shown. Initially the rod is vertical, it is slightly pushed and released. Find the angular velocity of rod and liner velocity of its one end when the rod becomes horizontal. Also calculate angular velocity of rod when it has rotated by an angle θ(θ<90∘).
This is the case of pure rotation

Applying energy consevation between (1) and (2), taking O as reference level
Mg(L2)=12I0ω2=12(ML23)ω2
ω=√3gL
Linear velocity of end A
vA=ωL=√3gL

Mg(L2)=Mg(L2)cosθ+12I0ω2
Mg(L2)(1−cosθ)=12×ML23ω2
ω=√3g(1−cosθ)L
Another method : When a rod makes an angle θ with vertical, torque acting on the rod about O
τ0=Mg(L2)sinθ=I0α=ML23α
α=3g2Lsinθ
ωdωdθ=3g2Lsinθ
∫ω0ωdω=3g2L∫ω0sinθdθ
ω22=3g2L|−cosθ|θ0
3g2L(1−cosθ)
ω=√3g(1−cosθ)L
Topper's Solved these Questions
Similar Questions
A uniform rod of mass M & length L is hinged about its one end as shown. Initially it is held vartical and then allowed to rotate, the angular velocity of rod when it makes an angle of 37∘ with the vertical is
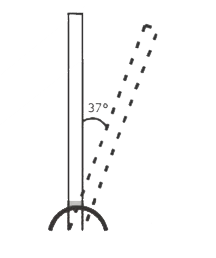
View SolutionA rod of length L is hinged from one end. It is brought to horizontal position and released. The angular velocity of the rod when it is in vertical position. Is
View Solution
Knowledge Check
A rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is
A√2gLB√3gLC√g2LD√gLA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, When it is in verticle position is
A√2gLB√3gLC√g2LD√gLA rod of mass m and length l is hinged at 'its' end and released from rest in position shown. Find the force exerted by the hinge when the rod becomes horizontal
 Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14
Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14
A rod od length l is moving in a vertical plane (x−y) when the owest point A of the rod is moved with a velociy v. find the a angular velocity of the rod and b velocity of the end B.

View SolutionA uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View SolutionA rod of length L is hinged from one end. It is brought to the horizontal position and released. The angular velocity of the rod when it is in the vertical position is √Kg/L. Then find the value of K.
View SolutionA rod of mass M and length L is falling vertically with speed v. Suddenly its one end gets stuck in a friciitonless hook. Find the angular velocity of the rod just after its end gets struck.

View SolutionA uniform rod of mass m and length l is on the smooth horizontal surface. When a constant force F is applied at one end of the rod for a small time t as shown in the figure. Find the angular velocity of the rod about its centre of mass.
View Solution

