A spherical conductor A contains two spherical cavities as shown in Fig.2.127. The total charge on conductor itself is zero . However , there is a point charge q1 at the center of one cavity and q2 at the center of the other cavity . Another charge q3 is placed at a large distance r from the center of the spherical conductor.

The force acting on conductor A will be
zero
q3(q1+q2)4πε0r2
−q3(q1+q2)4πε0r2
q3q1+q2q3+q1q24πε0r2
The correct Answer is:B
We see that that surface of two spherial cavities carries charges q1,−q2 respectively, and since the sphere A was not charged orginally, its sphereical surface must carry induced charges (q1+q2). Therefore, force acting on conductor A is q3(q1+q2)/4πε0r2
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Subjective type
Explore 7 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Multiple Correct
Explore 8 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 15 Videos
Similar Questions
A spherical conductor A contains two spherical cavities as shown in Fig.2.127. The total charge on conductor itself is zero . However , there is a point charge q1 at the center of one cavity and q2 at the center of the other cavity . Another charge q3 is placed at a large distance r from the center of the spherical conductor.

Which of the following statements are true ?
View SolutionA spherical conductor A contains two spherical cavities as shown in Fig.2.127. The total charge on conductor itself is zero . However , there is a point charge q1 at the center of one cavity and q2 at the center of the other cavity . Another charge q3 is placed at a large distance r from the center of the spherical conductor.

If q1 is displaced from its center slightly (being always inside the same cavity ), then the correct representation of field lines inside the same cavity is
View SolutionWhich one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
View SolutionA hollow spherical conductor of radius 1m has a charge of 250μC then electric intensity at a point distance of 0.5m from the centre of the spherical conductor is
View SolutionTwo spherical cavities of radii a and b are hollowed out from the interior of a neutral conducting sphere of radius R. At the center of each cavity , a point charge is placed . Call these charges qa and qb.
The electric field inside the cavity of radius a at a distance r from the center of cavity is

View SolutionA conducting spherical shell is earthed. A positive charge +q1 is placed at the center and another small positive charge +q2 is placed at a distance r from q1. Ignore the effect of induced charge due to q2 on the sphere. Then the coulomb force on q2 is
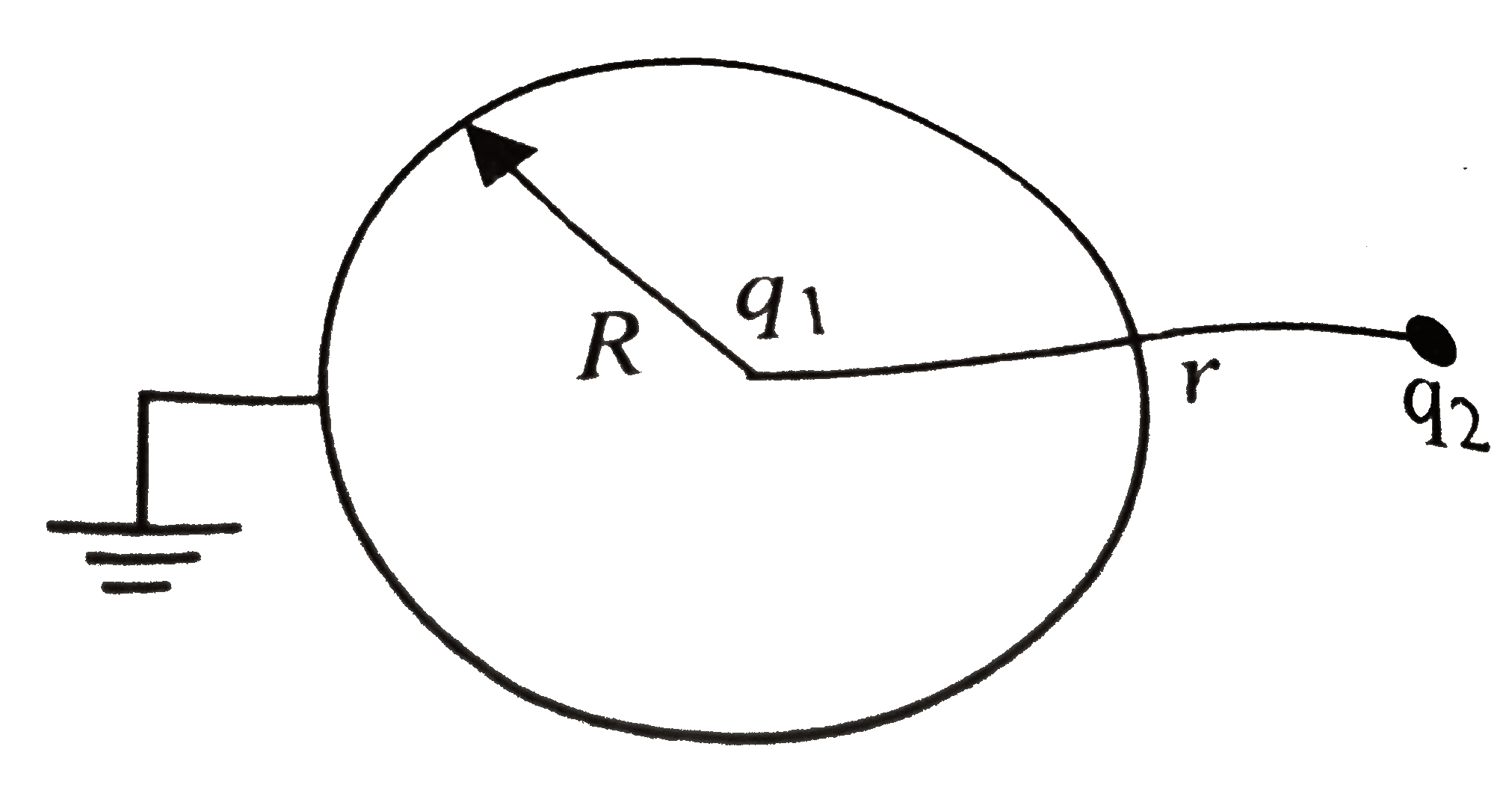
View SolutionIdentify A and B:
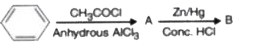
View SolutionA positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
View SolutionA conducting sphere of radius b has a spherical cavity with its centre displaced by 'a' from centre of sphere O1. A point charged q is placed at the centre of cavity O2. Q charge is given to conducting sphere and charge q0 is placed at P, a distance c from centre O1. Further O1,O2 and P are collinear

View SolutionA spherical conductor is placed near another positively charged conductor. The net charge acquired by spherical conductor will be
View Solution

