A rod of mass m and length l in placed on a smooth table. An another particle of same mass m strikes the rod with velocity v0 in a direction perpendicular to the rod at distance x(<l/2) from its centre . Particle sticks to the end. Let ω be the angular speed of system after collision , then
Find the maximum possible value of impulse (by varying x) that can be imparted to the particle during collision. Particle still sticks to the rod.
mv02
2mv03
3mv04
4mv05
The correct Answer is:A
To solve the problem, we need to analyze the situation step by step. We have a rod of mass m and length l on a smooth table, and a particle of the same mass m strikes the rod perpendicularly at a distance x from the center of the rod. The particle sticks to the end of the rod after the collision. We need to find the maximum possible impulse imparted to the particle during the collision by varying x.
Step 1: Understand the System
We have a rod and a particle, both of mass m. The particle strikes the rod with an initial velocity v0 at a distance x from the center of the rod. After the collision, the particle sticks to the rod, and we need to find the angular speed ω of the system.
Step 2: Conservation of Momentum
Before the collision, the momentum of the system is entirely due to the particle:
pinitial=mv0
After the collision, the total momentum of the system can be expressed in terms of the linear velocity v′ of the center of mass and the angular velocity ω:
pfinal=mv′+m(v′+ωl/2)
However, since the particle sticks to the end of the rod, we can simplify the analysis by focusing on the angular momentum about the center of the rod.
Step 3: Angular Momentum Conservation
The angular momentum before the collision about the center of the rod is:
Linitial=mv0⋅x
After the collision, the angular momentum is:
Lfinal=Iω
where I is the moment of inertia of the system. The moment of inertia of the rod about its center is 112ml2, and the moment of inertia of the particle at a distance l2 from the center is m(l2)2=14ml2. Therefore, the total moment of inertia I is:
I=112ml2+14ml2=13ml2
Step 4: Equate Angular Momenta
Setting the initial and final angular momentum equal gives:
mv0⋅x=13ml2ω
From this, we can solve for ω:
ω=3v0xl2
Step 5: Impulse Calculation
The impulse J imparted to the particle during the collision can be calculated as the change in momentum of the particle:
J=mv′−mv0
The final velocity v′ of the particle after the collision can be expressed in terms of ω and the distance from the center:
v′=v0−ωx
Substituting ω from Step 4:
v′=v0−3v0x2l2
Thus, the impulse becomes:
J=m(v0−3v0x2l2)−mv0=−m3v0x2l2
Step 6: Maximizing the Impulse
To find the maximum impulse, we need to maximize −3v0x2l2. Since x<l2, the maximum value occurs at the maximum value of x, which is x=l2:
Jmax=−m3v0(l2)2l2=−m3v0l24l2=−3mv04
Final Answer
The maximum possible value of the impulse imparted to the particle during the collision is:
Jmax=3mv04
We have a rod and a particle, both of mass m. The particle strikes the rod with an initial velocity v0 at a distance x from the center of the rod. After the collision, the particle sticks to the rod, and we need to find the angular speed ω of the system.
Before the collision, the momentum of the system is entirely due to the particle:
pinitial=mv0
After the collision, the total momentum of the system can be expressed in terms of the linear velocity v′ of the center of mass and the angular velocity ω:
pfinal=mv′+m(v′+ωl/2)
However, since the particle sticks to the end of the rod, we can simplify the analysis by focusing on the angular momentum about the center of the rod.
The angular momentum before the collision about the center of the rod is:
Linitial=mv0⋅x
After the collision, the angular momentum is:
Lfinal=Iω
where I is the moment of inertia of the system. The moment of inertia of the rod about its center is 112ml2, and the moment of inertia of the particle at a distance l2 from the center is m(l2)2=14ml2. Therefore, the total moment of inertia I is:
I=112ml2+14ml2=13ml2
Setting the initial and final angular momentum equal gives:
mv0⋅x=13ml2ω
From this, we can solve for ω:
ω=3v0xl2
The impulse J imparted to the particle during the collision can be calculated as the change in momentum of the particle:
J=mv′−mv0
The final velocity v′ of the particle after the collision can be expressed in terms of ω and the distance from the center:
v′=v0−ωx
Substituting ω from Step 4:
v′=v0−3v0x2l2
Thus, the impulse becomes:
J=m(v0−3v0x2l2)−mv0=−m3v0x2l2
To find the maximum impulse, we need to maximize −3v0x2l2. Since x<l2, the maximum value occurs at the maximum value of x, which is x=l2:
Jmax=−m3v0(l2)2l2=−m3v0l24l2=−3mv04
The maximum possible value of the impulse imparted to the particle during the collision is:
Jmax=3mv04
Topper's Solved these Questions
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Matrix Matching Type Questions
Explore 16 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:More than one option is correct
Explore 36 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
Similar Questions
A rod of mass m and length l in placed on a smooth table. An another particle of same mass m strikes the rod with velocity v0 in a direction perpendicular to the rod at distance x(<l/2) from its centre . Particle sticks to the end. Let ω be the angular speed of system after collision , then
As x is increased from 0 to l/2 , the angular speed ω.
View SolutionA uniform rod AB of length L and mass M is lying on a smooth table. A small particle if mass m strike the rod with velocity v0 at point C at a distance comes to rest after collision. Then find the value of x, so that point A of the rod remains stationary just after collision.
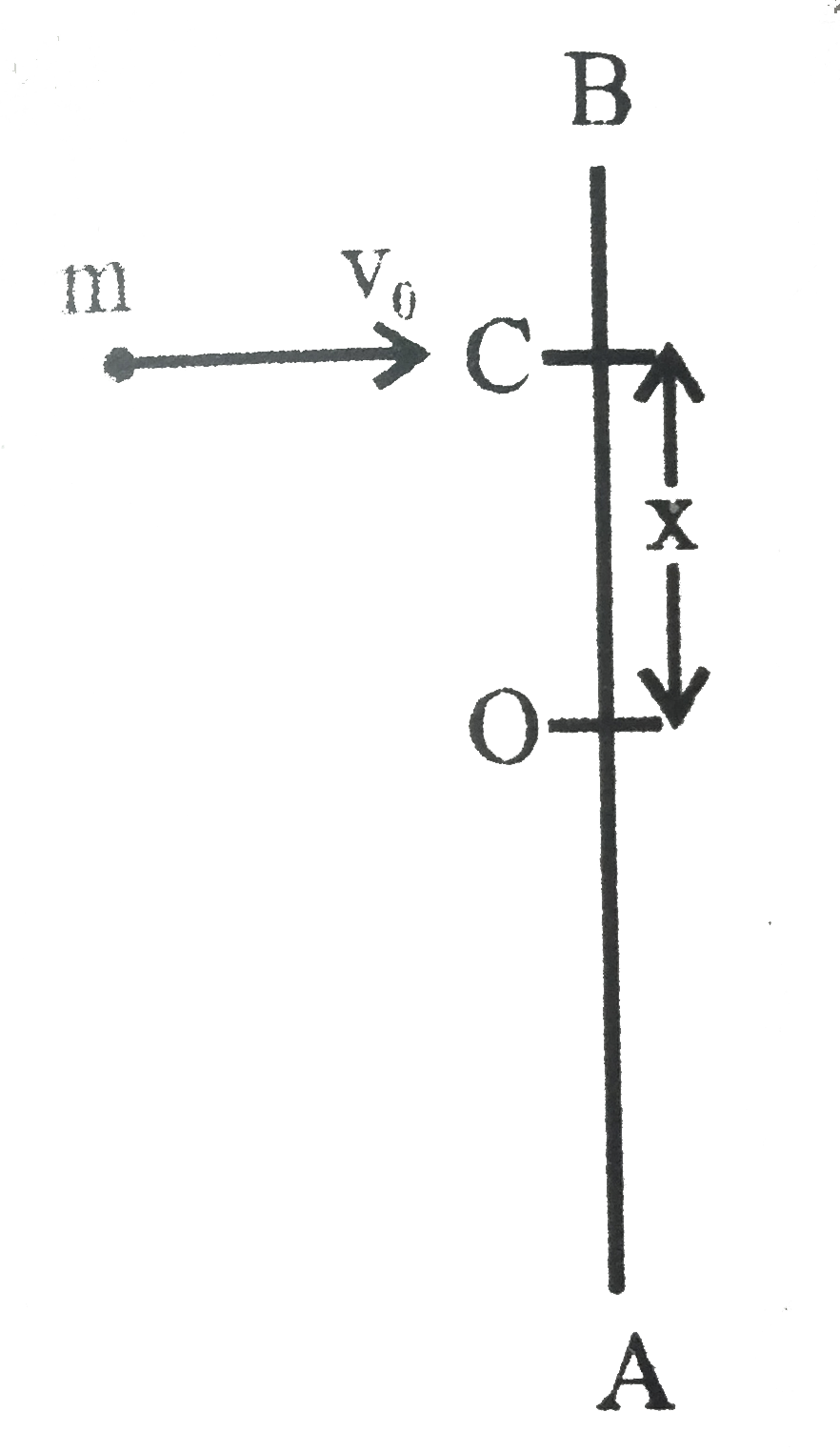 .
.
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
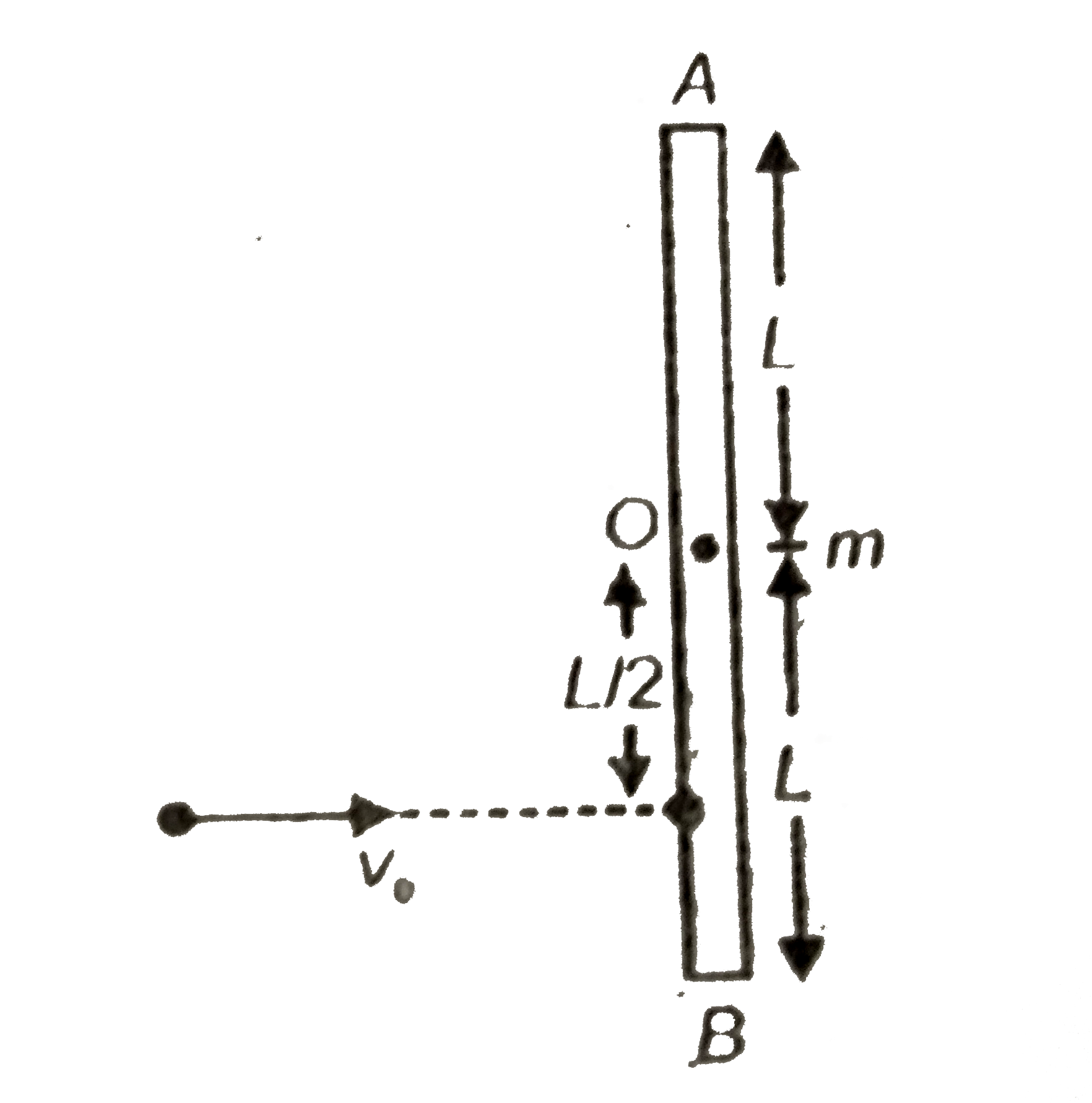
Angular velocity of rod just after collision is
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.

Angular velocity of rod just after collision is
View SolutionA Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.
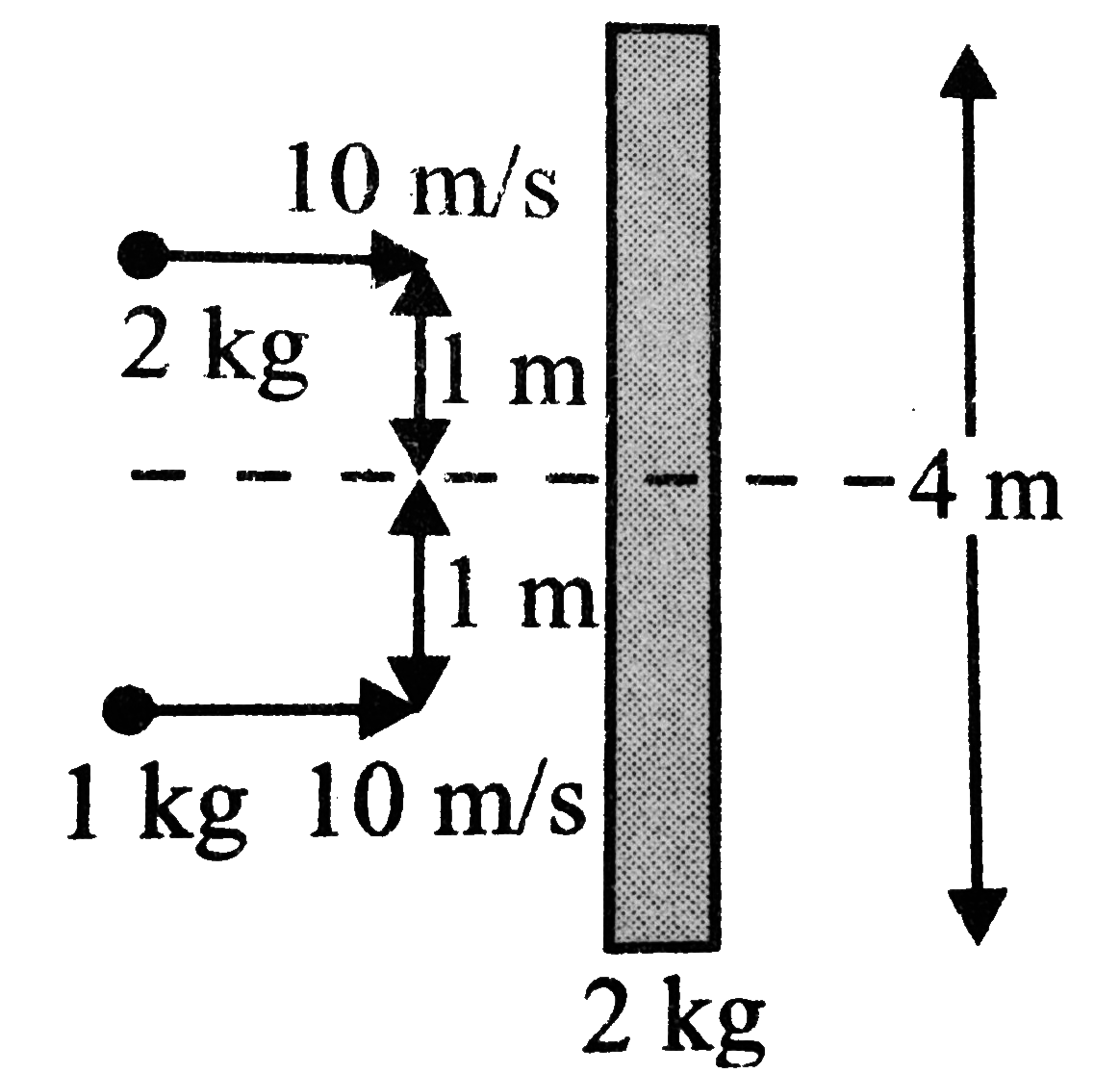
Velocity of the centre of mass of the rod after collision is
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:


View SolutionA uniform rod of mass 2kg and length 1m lies on a smooth horizontal plane. A particle of mass 1 kg moving at a speed of 2ms−1 perpendicular to the length of the rod strikes it at a distance 14 m from the centre and stops . Find the angular velocity of the rod about its centre just after the collision (in rad/s)
View SolutionThe radius of gyration of a uniform rod of mass m and length l about an axis perpendicular to its length and at distance l4 from its centre will be
View Solution

