A particle of mass m=1kg collides with the end with velocity v0=6ms−1 of a spinning rod of mass2m and length l=1m at the end of the rod. If the coefficient of restitution of collision e=(2/3), find the
a. velocity of the particle
b. angular velocity of the rod just after the impact.
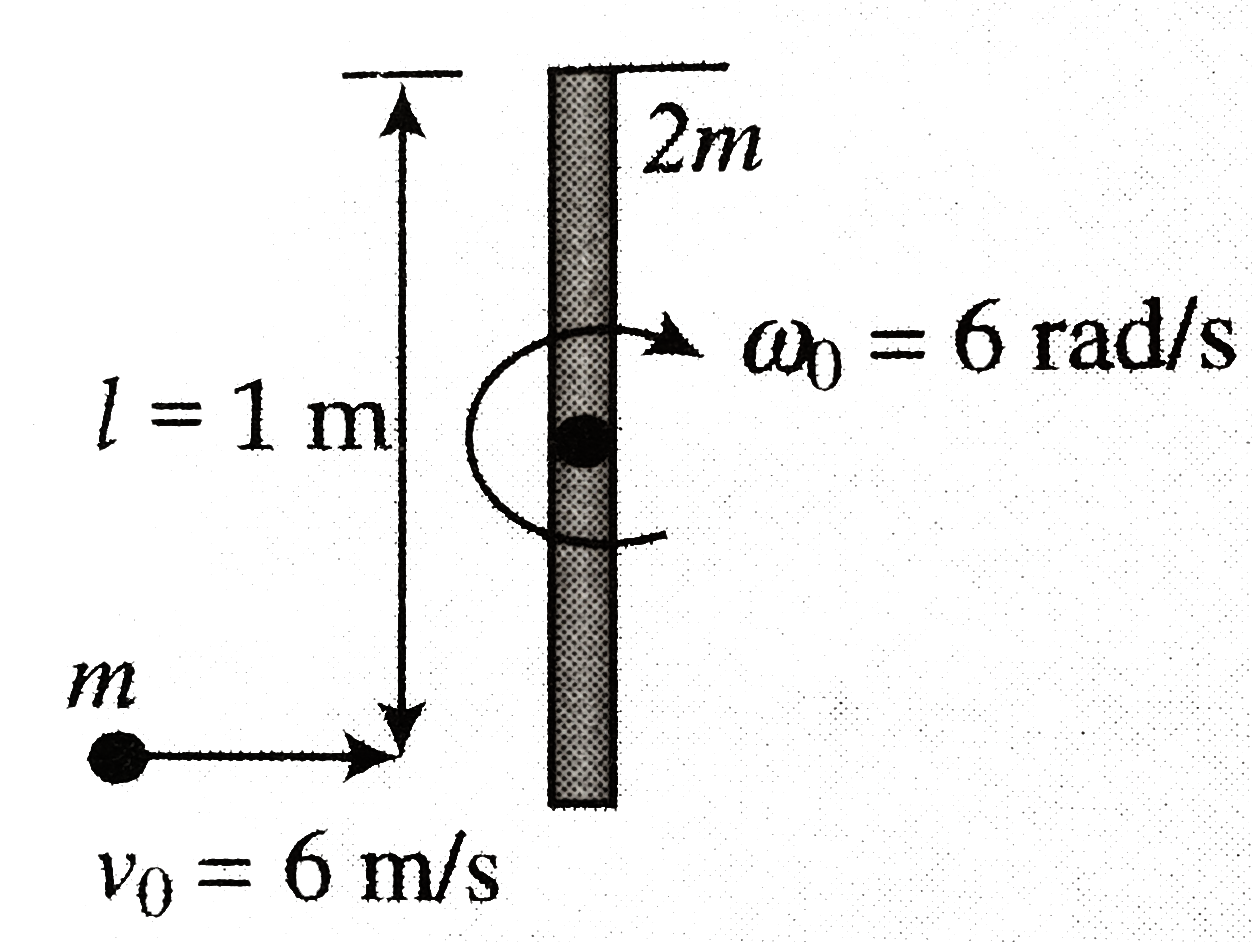
If we take rod and particle as system we find no external impulse acting on the sytem. Hence, we can use conservation of linear moemntum just before collision just after collision. Let the velocities of particle and rod just after collision is v1 and v2 respectively.
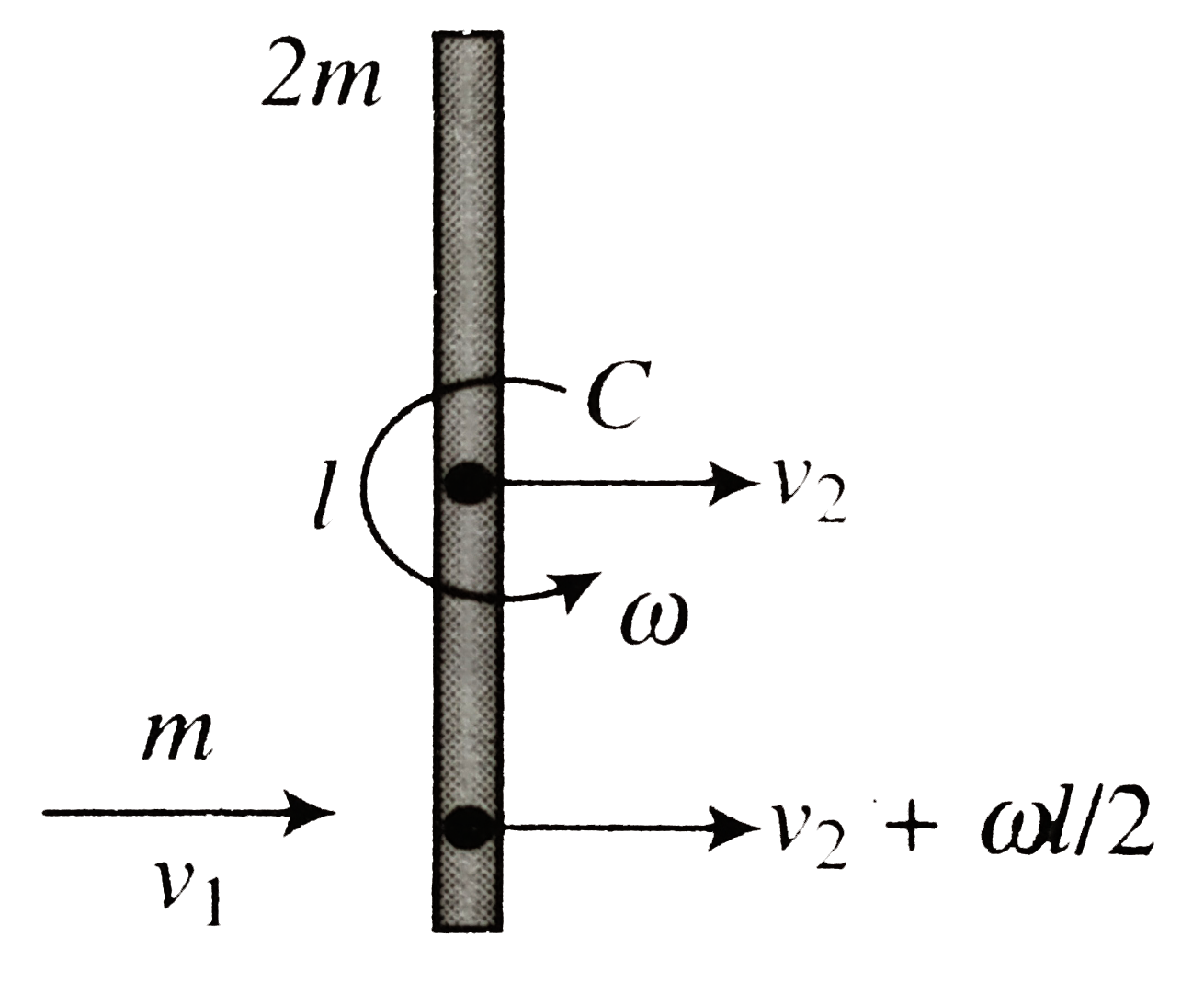
mv1+2mg2=mv0
v1+2v2=6..........i
No applying Newton's restitution equation at the point of collision.
e=22=(v2+ωl)=v1v0−(−ω0l2)
2.(6+3)=3v2+3ω2−3v1
36=6v23ω−6v1.........ii
Conservation of angular momentum about point of collision
−2ml212.ω0=2ml212.ω−2mv2.l2
−ω0l=ωl−6v2⇒ω=6v2−6..........iii
Put the value of ω in ii , 36=6v2+18v2−18−6v1
v1−4v2=9.......iv
From i and iii v1=1ms−1,v2=2.5ms−1 and ω=9rads−1
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples12videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.111videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A uniform rod of lengh l moving with a downward velocity v0 strikes a peg P. If the coefficient of restitutioin of impact is e, find the velocity of CM of the rod just after impact.
 View Solution
View SolutionA glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View SolutionA block of mass m moving at a velocity υ collides head on with another block of mass 2m at rest. If the coefficient of restitution is 1/2, find the velocities of the blocks after the collision.
View SolutionIn the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be
 View Solution
View SolutionA particle of mass m collides with another stationary particle of mass M such that the second particle starts moving and the first particle stops just after the collision. Then which of the following conditions must always be valid ?
View SolutionA ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View SolutionA ball of mass m moving with velocity u collides head-on which the second ball of mass m at rest. If the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View SolutionA rod of length l is moving in a vertical plane (x−y) when the lowest point A of the rod is moved with a velocity v. find the a angular velocity of the rod and b velocity of the end B.
 View Solution
View SolutionTwo spherical bodies of mass m1 and m2 fall freely through a distance h. before the body m2 collides with the ground. If the coefficient of restitution of all collisions is e, find the velocity of m1 just after it collides with m2
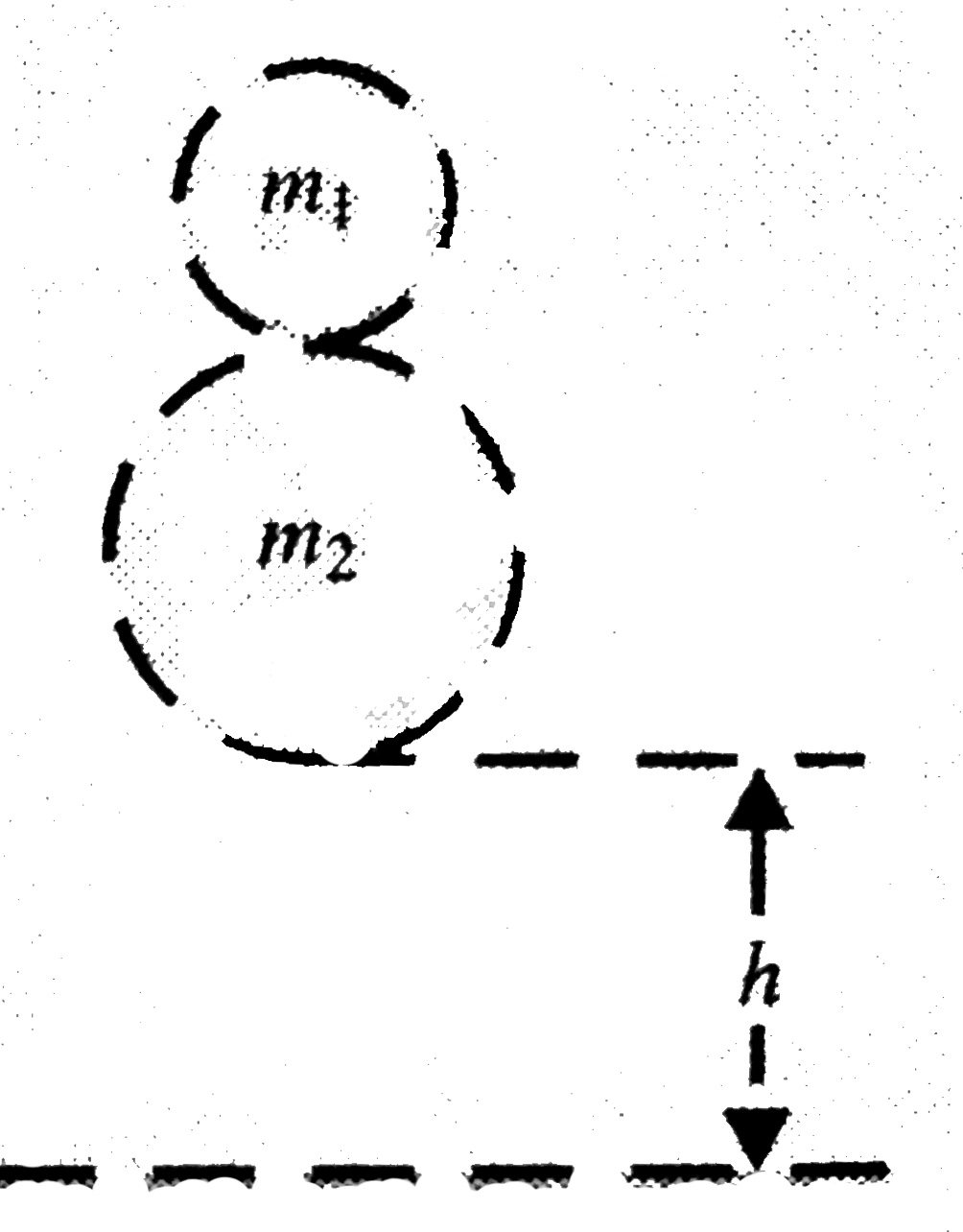 View Solution
View SolutionA uniform rod of mass m and length l is released from rest from its vertical position by giving a gently push. In consequence, the end of the rod collides at P after rotating about the smooth horizontal axis O. If the coefficient of restitution e=(12). Find the: a. angular speed of the rod just after the impact.
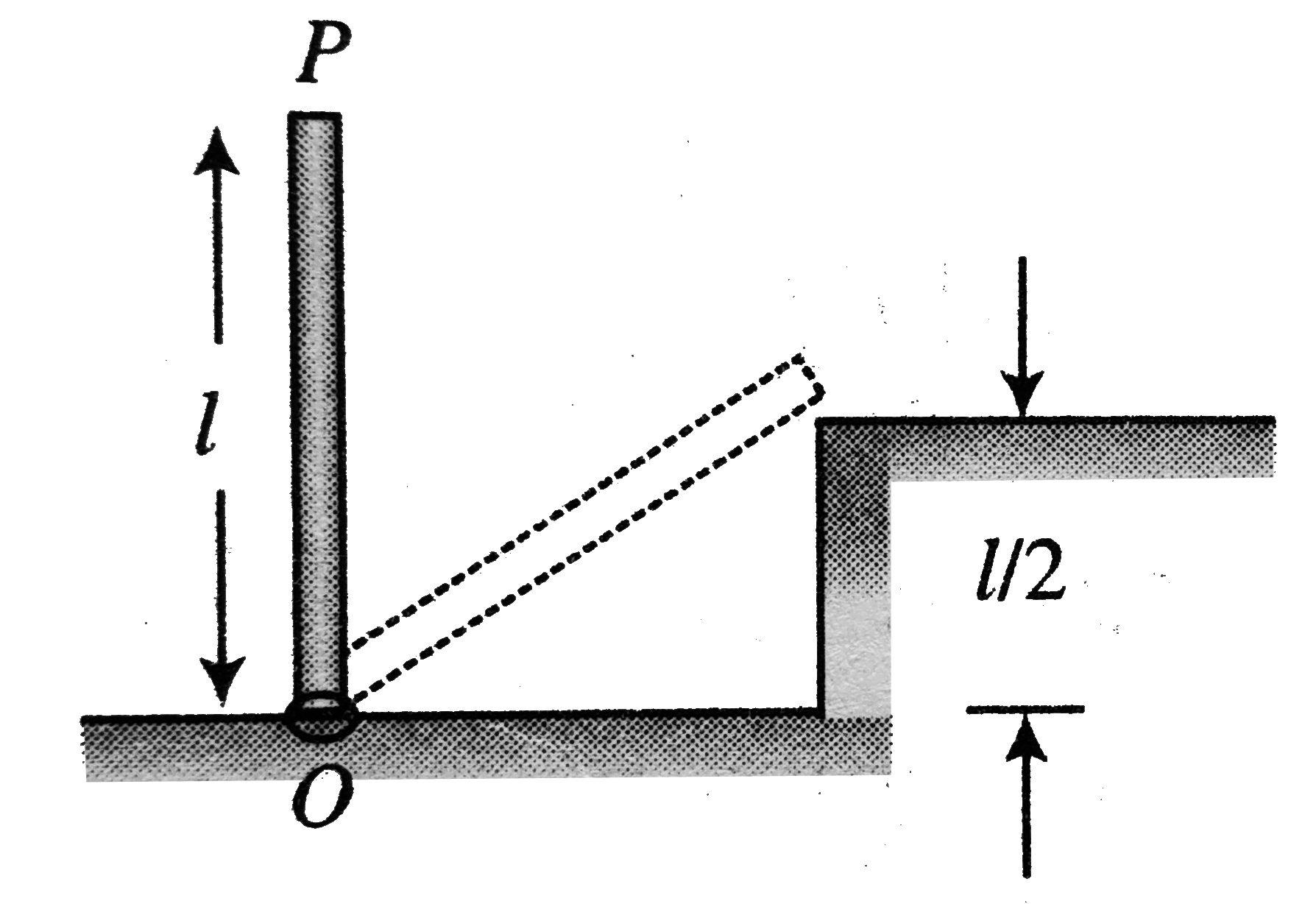
b. energy loss during collision. c. maximum angle rotated by rod after collision.View Solution


