A uniform rod of lengh l moving with a downward velocity v0 strikes a peg P. If the coefficient of restitutioin of impact is e, find the velocity of CM of the rod just after impact.

Method 1: At the time of impact the force acting on the rod is N (upward) and mg (downward). Since normal reaction is an ampulsive force during impact, N>>mg. Then we disregard the effect of gravity during the impact.
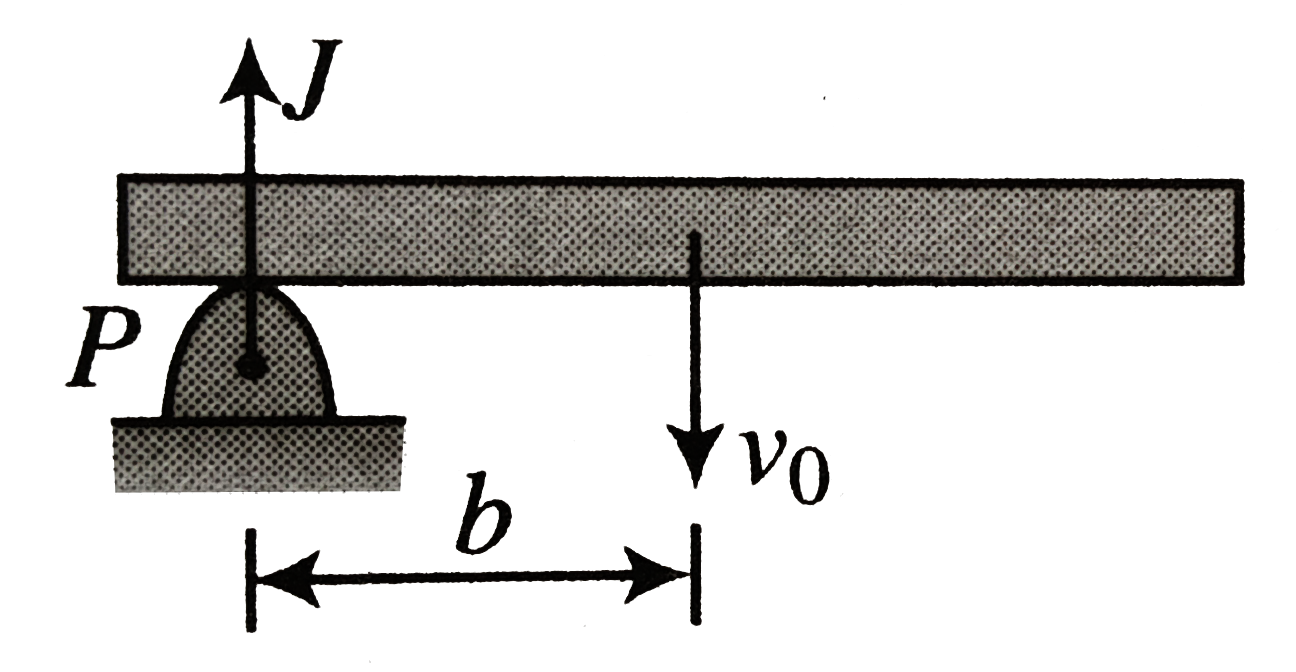
Impulse equation mv0=J=mv ..........i
The angular impulse of N is J.b=ml212ω
J=ml212bω...........ii
Adding eqn i and ii we have
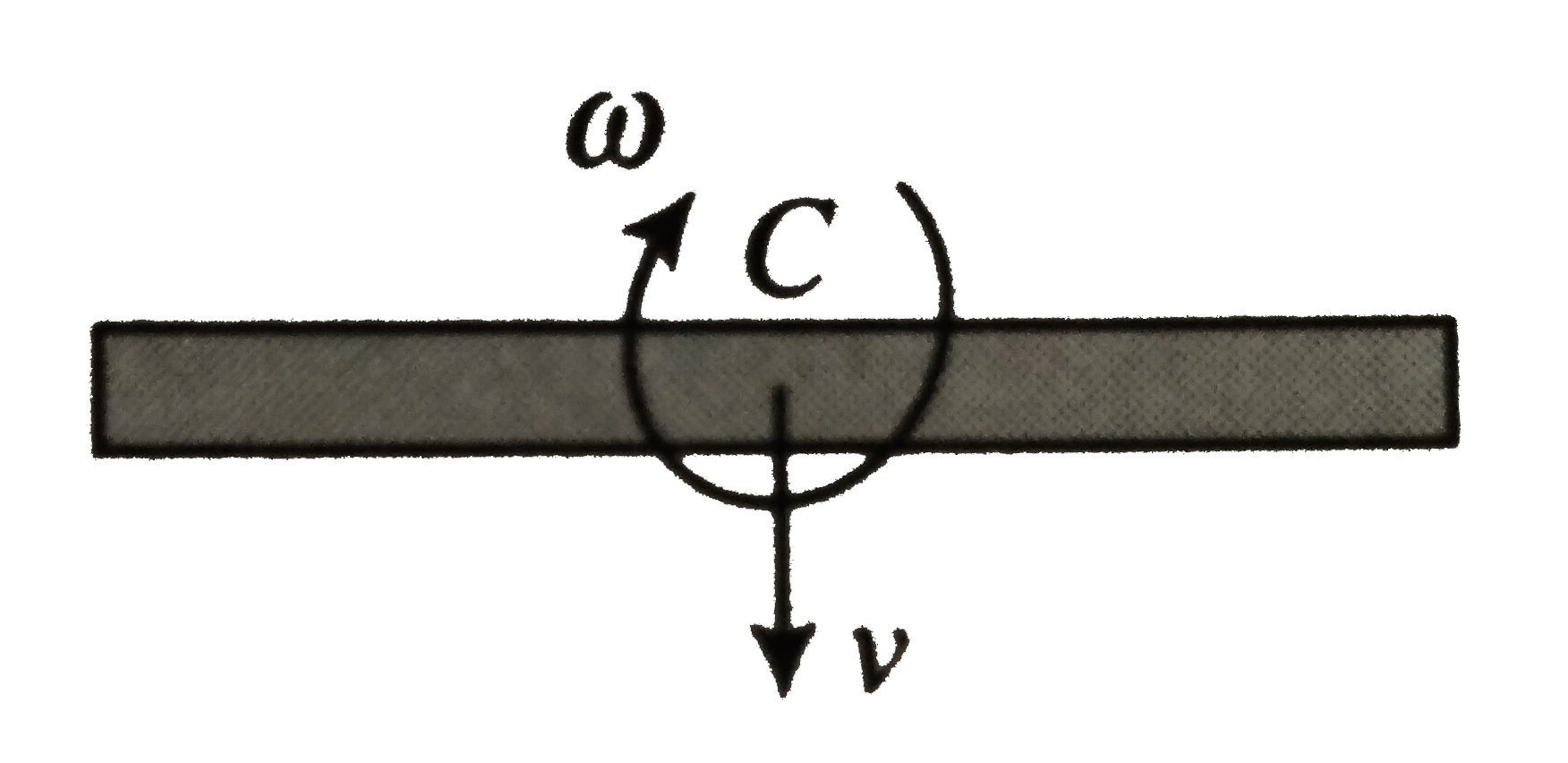
v0−v=l2ω12b.............iii
Newton's empirical formula gives us
vp=−v0 ..........iv
The velocity of P is →vP=→vPC+→vC
v−bω=−ev0..............v
Now we have two equan ii and iv for two unknowns v and ω,.
Solving these two equations we have v=12b2−el212b2+l2v0
Method 2: If we choose the fixed point at P, the angular impulse about P is zero because the impusle J passes through P during impact.
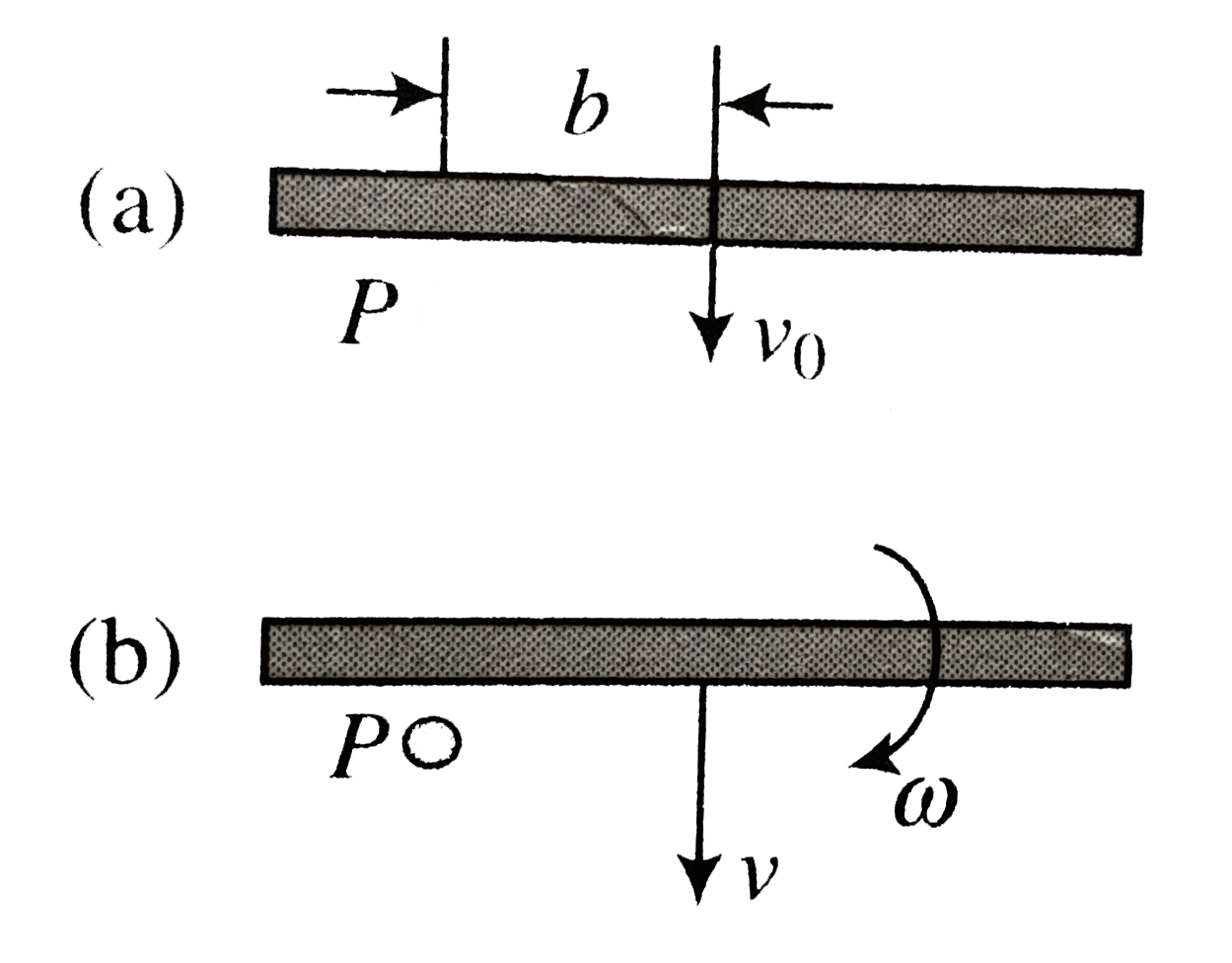
hence the angular momentum of the rod just before and just after the impact about remain constant.
→L1=→L2, where →L1=mv0b(−ˆk)
and →L2=ml212ω(−ˆk)+mvb(−ˆk)
Then mv0b=mvb+ml212ω
This gives v0−v=l2ω12b
The other equations remain as unchanged. Solving the above eqn we will obtain the same value of v.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
An elastic ball of mass 'm' is suspended from a fixed point by an inextensible string. A small particle of same mass m, moving downwards at an angle of 37∘ with the vertical lits the ball directly with the velocity v0. If the coefficient of restitution is 4/5,
(i) find the velocity of the ball just after the impact.
(ii) determine the impulsive tension(i.e impulse) in the string at the instant of collision.
View SolutionA particle of mass m=1kg collides with the end with velocity v0=6ms−1 of a spinning rod of mass2m and length l=1m at the end of the rod. If the coefficient of restitution of collision e=(2/3), find the
a. velocity of the particle
b. angular velocity of the rod just after the impact.
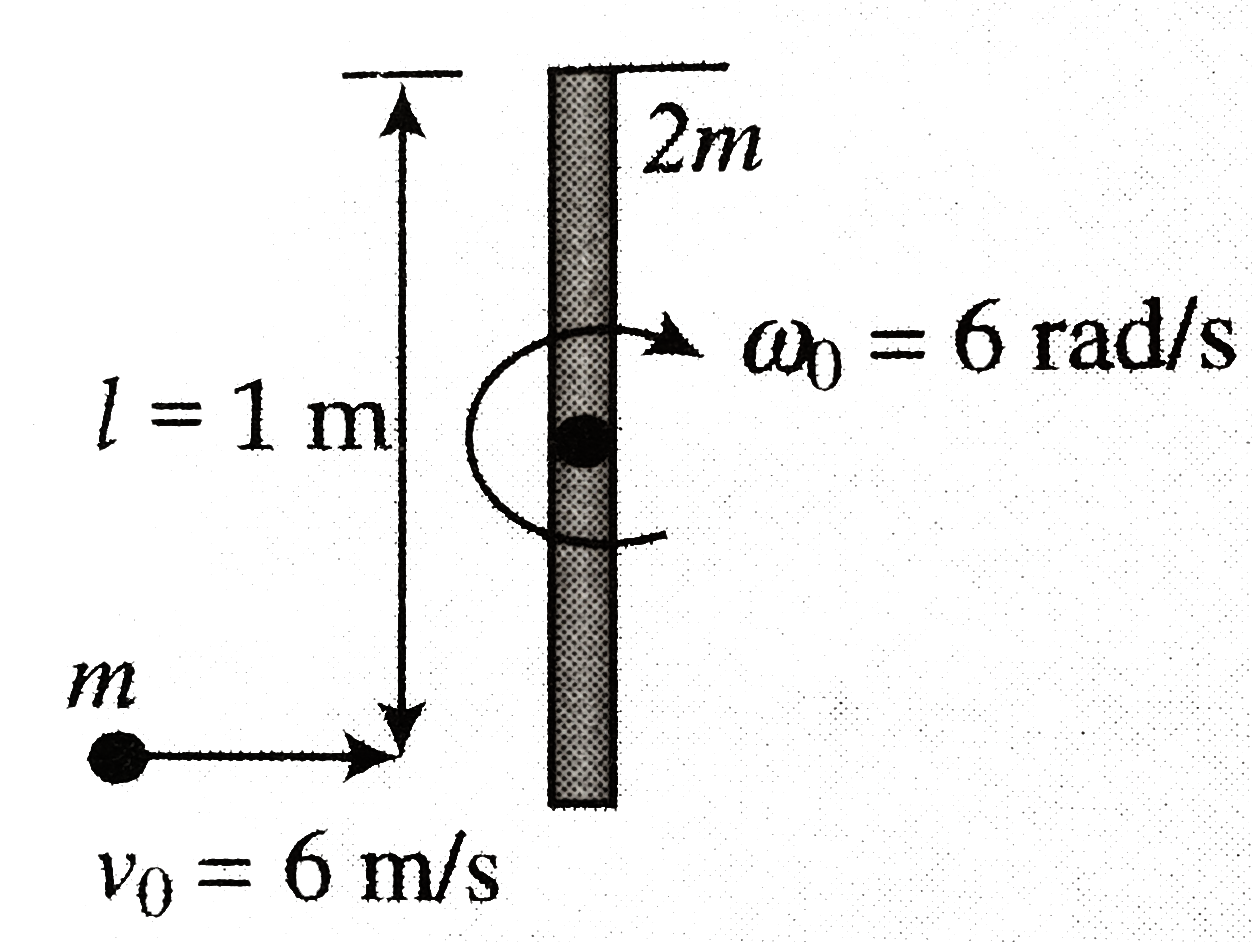
View SolutionA uniform rod of length l is spinning with an angular velocity ω=2vl while its centre of mass moves with a velocity v. Find the velocity of the end of the rod.

View SolutionA ball collides with a frictionless wall with velocity u as shown in the figure. Coefficient of restitution for the impact is e.
(a) Find expression for the velocity of the ball immediately after the impact.
(b) If impact is perfectly elastic what do you observe?
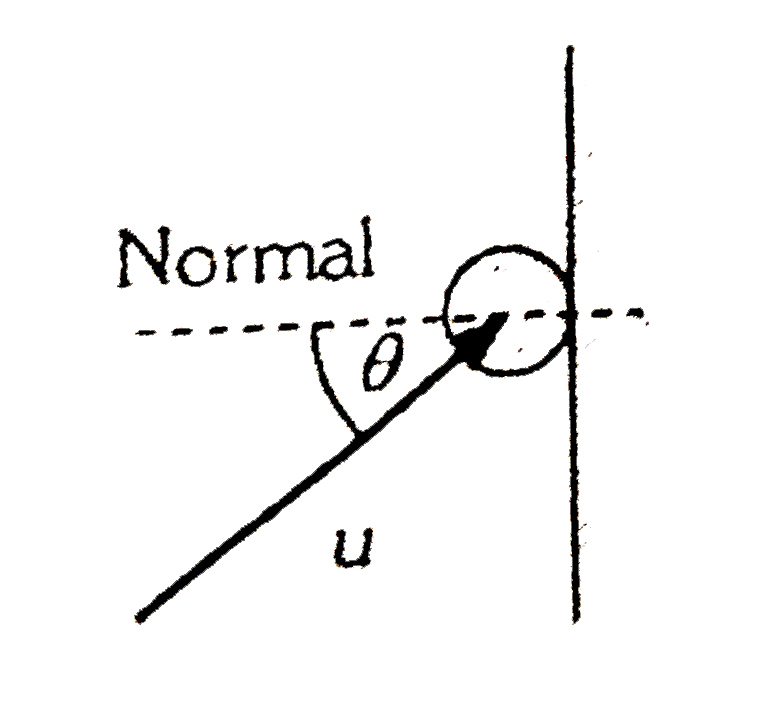
View SolutionA uniform rod of mass m and length l is released from rest from its vertical position by giving a gently push. In consequence, the end of the rod collides at P after rotating about the smooth horizontal axis O. If the coefficient of restitution e=(12). Find the: a. angular speed of the rod just after the impact.
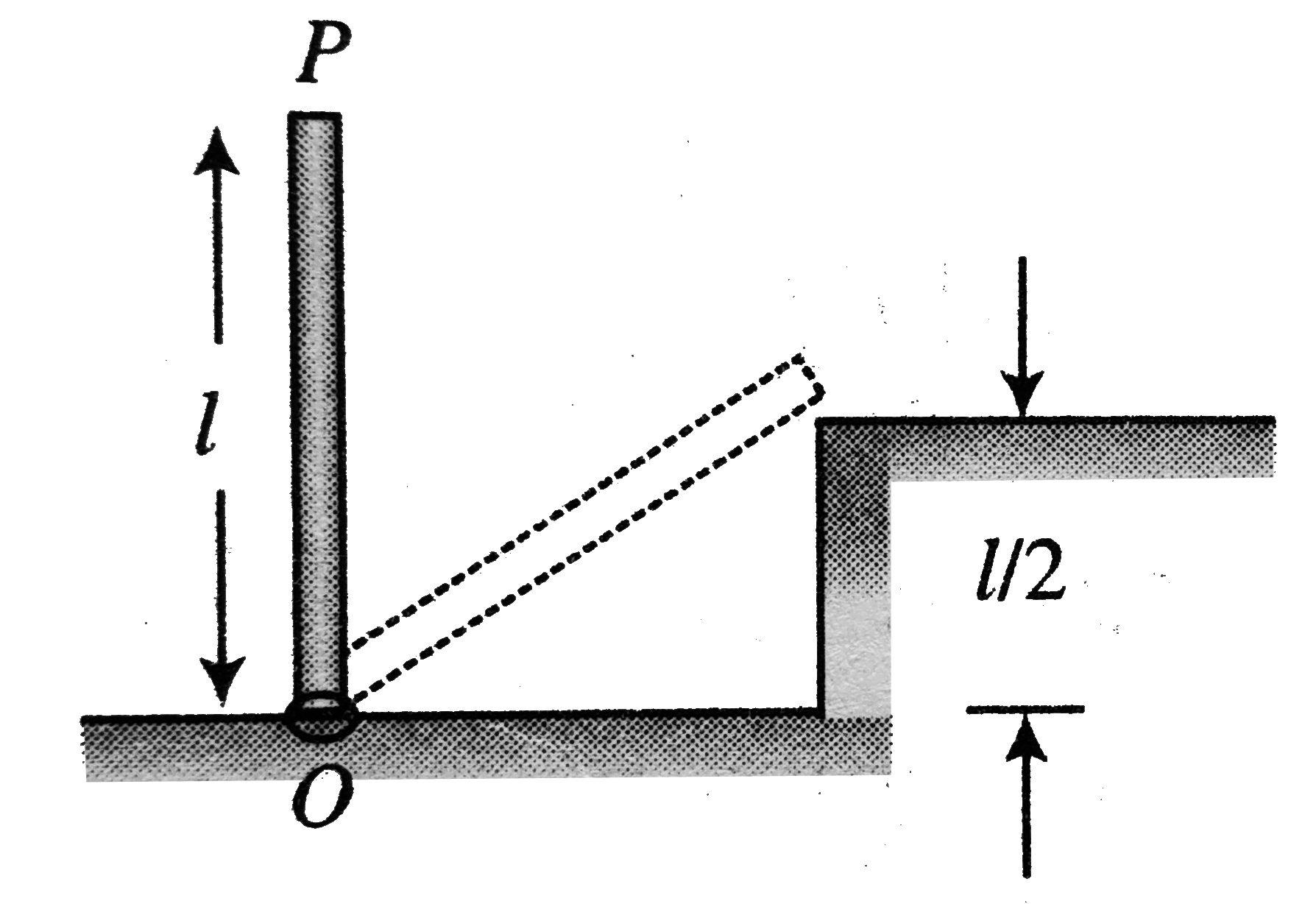
b. energy loss during collision. c. maximum angle rotated by rod after collision.
View SolutionA homogenous rod of length l=ηx and mass M is lying on a smooth horizontal floor. A bullet of mass m hits the rod at a distance x from the middle of the rod at a velocity v0 perpendicular to the rod and comes to rest after collision. If the velocity of the farther end of the rod just after the impact is in the opposite direction of v0, then:
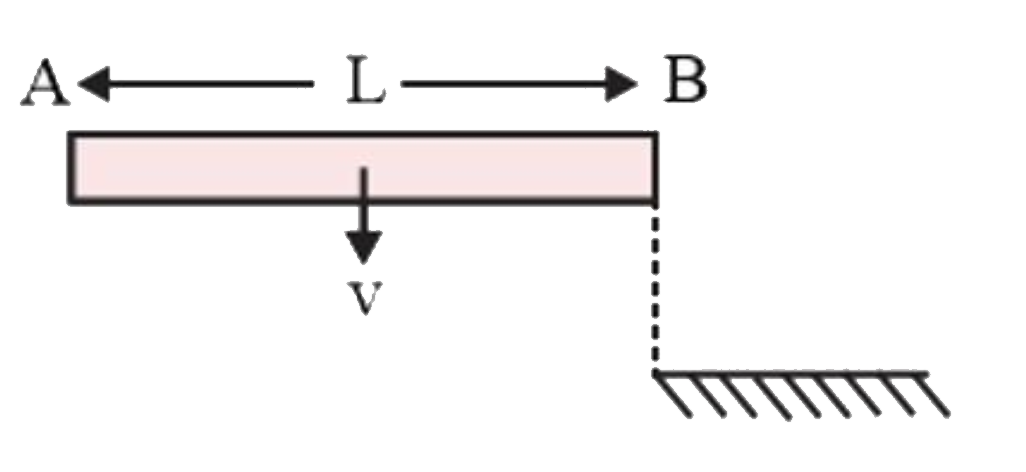
View SolutionA rod AB of length L and mass M is free to move on a frictionless horizontal surface. It is moving with a velocity v, as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact, the angular velocity of the rod AB, just after impact, is
View SolutionA rod of length l is moving in a vertical plane (x−y) when the lowest point A of the rod is moved with a velocity v. find the a angular velocity of the rod and b velocity of the end B.

View SolutionA glass rod of length l moves with velocity v in a uniform magnetic field B. What is the e.m.f induced in the rod?
View SolutionA rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle, of mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a speed of v0/4. Find the following: a. The ratio M/m. b. The angular velocity of the rod about O. c. The coefficient of restitution 'e' for the collision. d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
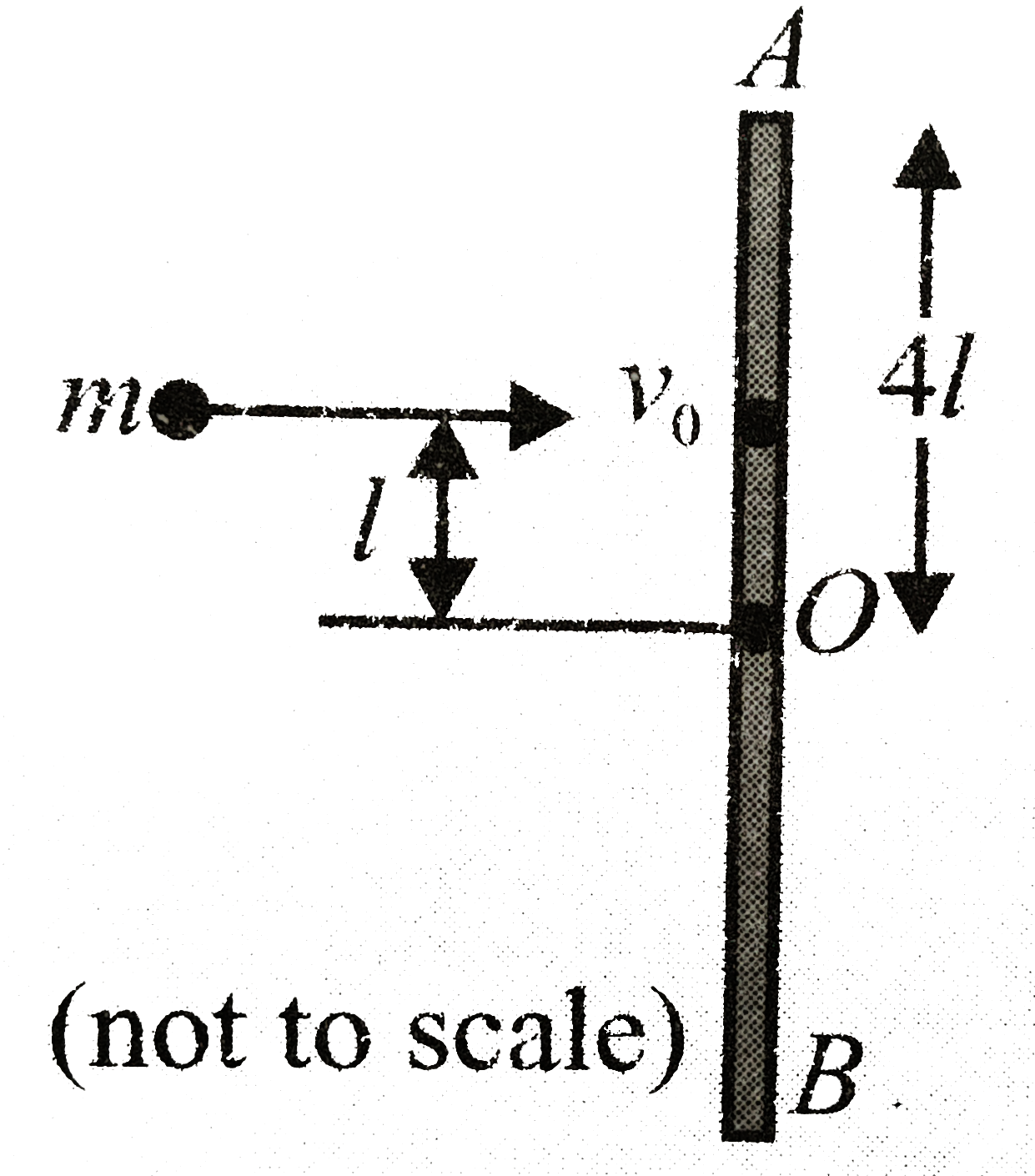
View Solution
