A particle is projected up the inclined plane strikes the plane at right angles. Find the relation between angle of inclination of the plane and angle of projection from the inclined plane.

If the particle strikes the plane perpendicular , then
vx=0=>vx=ux+axt⇒0=ucosθ−gsinαT
Putting , T=2usinθgcosα⇒ucosθ=gsinα(2usinθgcosα)
⇒2tanθ=cotα
Topper's Solved these Questions
- KINEMATICS Book:MTG GUIDEChapter:KINEMATICS Exercise:Topicwise Practice Questions (DISTANCE AND DISPLACEMENT)
Explore 2 Videos
- KINEMATICS Book:MTG GUIDEChapter:KINEMATICS Exercise:Topicwise Practice Questions (SPEED AND VELOCITY)
Explore 9 Videos
- GRAVITATIONBook:MTG GUIDEChapter:GRAVITATIONExercise:AIPMT/NEET MCQS
Explore 32 Videos
- LAWS OF MOTIONBook:MTG GUIDEChapter:LAWS OF MOTIONExercise:AIPMT /NEET (MCQ)
Explore 24 Videos
Similar Questions
Knowledge Check
A particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .A2u2√3+13g.B4u2√3−19g.C2u2√5−18g.D2u2√3−13g
.A2u2√3+13g.B4u2√3−19g.C2u2√5−18g.D2u2√3−13gBy increasing the angle of inclination, the M.A. of an inclined plane
Adecreases.Bincreases.Cremains the same.Ddepends on the load to be raised.
Downward Projection On An Inclined Plane
View SolutionA particle is projected up an inclined plane of inclination β at an elevation ∝ to nthe horizontal. Find the ratio between tan∝andtanβ, if the particle strikes the plane horizontally.
View SolutionA particle is projected up an inclined plane of inclination β at an elevation ∝ to the horizontal. Find the ratio between tan∝andtanβ, if the particle strikes the plane horizontally.
View SolutionFor a given velocity of projection from a point on the inclined plane, the maximum range down the plane is three times the maximum range up the incline. Then find the angle of inclination of the inclined plane.
View SolutionFor a given velocity of projection from a point on the inclined plane, the maximum range down the plane is three times the maximum range up the incline. Then find the angle of inclination of the inclined plane.
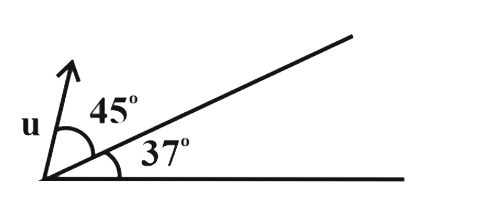
View SolutionA particle is projected on a frictionless inclined plane of inclination 37∘ at an angle of projection 45∘ from the inclined plane as shown in the figure. If after the first collision from the plane, the particle returns to its point of projection, then what is the value of the reciprocal of the coefficient of restitution between the particle and the plane?
View Solution

