A cylinder of mass M and radius R starts falling under gravity at t = 0 as shown in the figure . Calculate
(i) tension in the massless string
(ii) acceleration of the cylinder
(iii) instantaneous power developed by gravitational force .

(i) Equation of motion of the cylinder
Mg−2T=MaorMg=Ma+2T …(i)
Torque τ=Iα=RF
or (12MR2)aR=R(2T)ora=4TM
or M4TM+2T=Mg (from equation (i))
orT=Mg6
(ii) Acceleration of cylinder (a)
∵a=4TM and T=Mg6
∴a=2g3
(iii) Instantaneous Power .
Power P = Force (F) × velocity (v)
or P=Mg×at[∵v=u+at=0+at]
or P =Mg×(2g3)t or Power = 2/3 Mg2t.
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY Book:MTG GUIDEChapter:MOTION OF SYSTEM OF PARTICLES AND RIGID BODY Exercise:NEET CAFE (TOPICWISE PRACTICE QUESTIONS )
Explore 140 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY Book:MTG GUIDEChapter:MOTION OF SYSTEM OF PARTICLES AND RIGID BODY Exercise:CHECK YOUR NEET VITALS
Explore 14 Videos
- LAWS OF MOTIONBook:MTG GUIDEChapter:LAWS OF MOTIONExercise:AIPMT /NEET (MCQ)
Explore 24 Videos
- OSCILLATIONS AND WAVES Book:MTG GUIDEChapter:OSCILLATIONS AND WAVES Exercise:AIPMT / NEET MCQs
Explore 43 Videos
Similar Questions
A cylinder of mass 0.6kg and radius R is falling under gravity without slipping as the thread is unfolding.Find the tension in the thread (in newton).
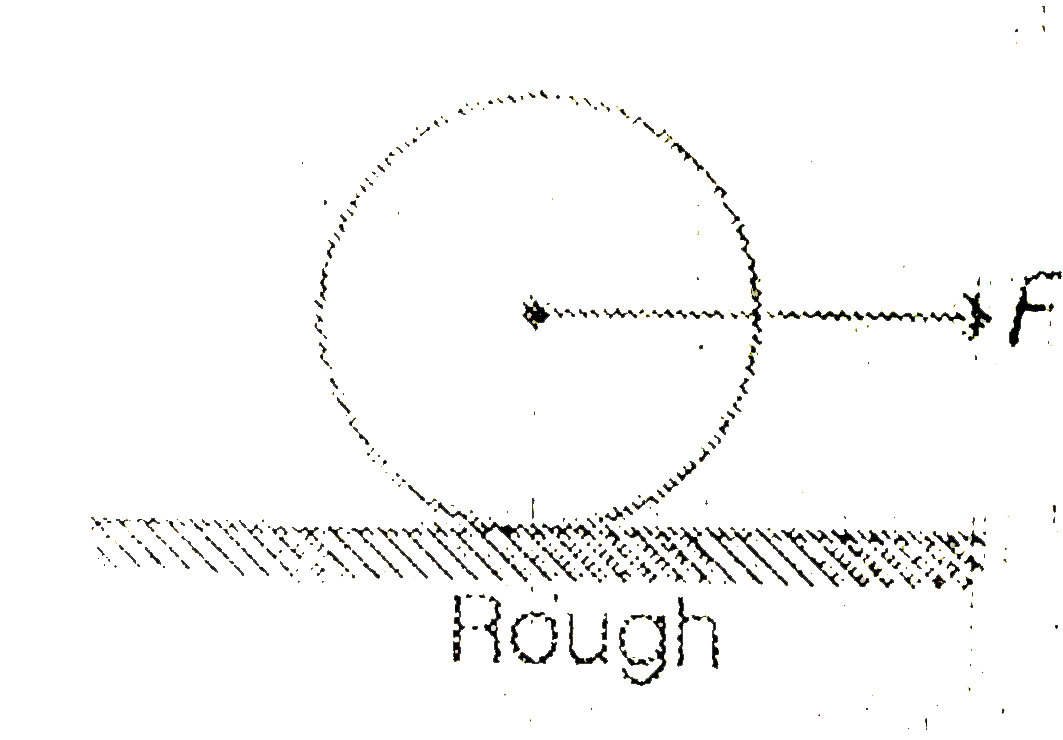
View SolutionA solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).
View Solution
Knowledge Check
A solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).
 AThe acceleration of the centre of mass is FMBThe acceleration of the centre of mass is 23FMCThe friction force on the cylinder acts backwardDThe magnitude of the friction force is F3
AThe acceleration of the centre of mass is FMBThe acceleration of the centre of mass is 23FMCThe friction force on the cylinder acts backwardDThe magnitude of the friction force is F3
A uniform cylinder of mass m and radius R starts descending at a moment t=0 due to gravity, Neglecting the mass of the thread, find
(a) the tension of each thread and the angular acceleration of the cylinder,
(b) the time dependence of the instantaneous power developed by the gravitational force.

View SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.
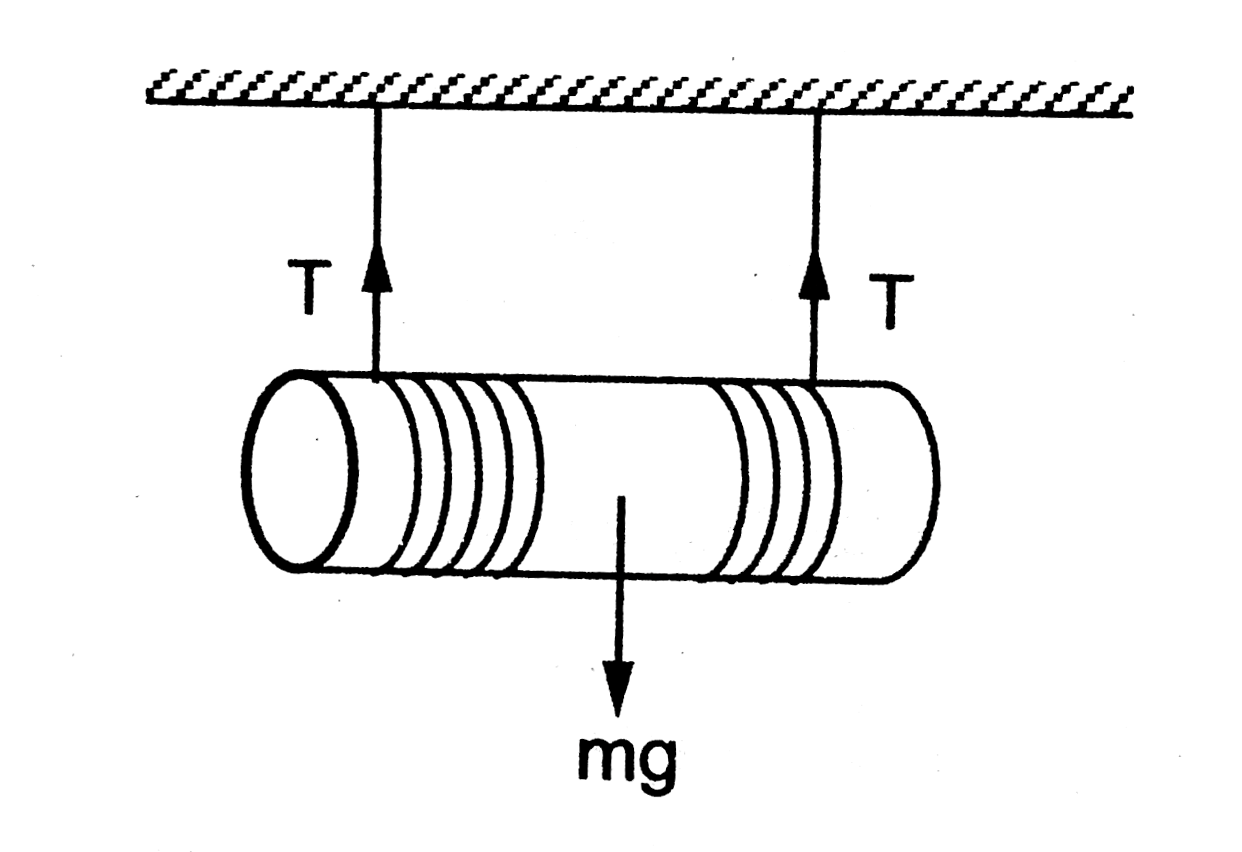
View SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.

View SolutionA body of mass 5kg is attached to a weightless string wound round a cylinder of mass 8kg and radius 0.3m. The body is allowed to fall. Calculate (i) tension in the string, (ii) acceleration with which the body falls and (iii) angular acceleration of the cylinder.
View SolutionA body of mass 5 kg is attached to a weightless string wound round a cylinder of mass 8 kg and radius 0.3 m. The body is allowed to fall. Calculate (i) tension in the string (ii) acceleration with which the body falls and (iii) the angular acceleration of the cylinder.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View Solution

