A cell sends a current through a resistance R1 for time t, next the same cell sends current through another resistance R2 for the time t If the same amount of heat is developed in both the resistance then find the internal resistance of the cell
r=√R1+R2
r=√R1×R2
r=R1+R22
r=1R2+1R2
The correct Answer is:B
To solve the problem step by step, we will use the concepts of electric circuits, specifically focusing on the heat generated in resistors when current flows through them.
Step 1: Understanding the Problem
We have a cell that sends a current through two different resistances R1 and R2 for the same amount of time t. The heat generated in both resistances is the same. We need to find the internal resistance r of the cell.
Step 2: Formula for Heat Developed
The heat developed H in a resistor when a current I flows through it for time t is given by:
H=I2Rt
where R is the resistance.
Step 3: Current Through the Resistor
The current I flowing through a resistor connected to a cell with voltage V and internal resistance r can be expressed as:
I=VR+r
where R is the external resistance.
Step 4: Heat Developed in Each Resistance
For the first resistance R1:
H1=I21R1t=(VR1+r)2R1t
For the second resistance R2:
H2=I22R2t=(VR2+r)2R2t
Step 5: Setting the Heat Developed Equal
Since the heat developed in both resistances is the same:
H1=H2
This gives us:
(VR1+r)2R1t=(VR2+r)2R2t
Step 6: Simplifying the Equation
We can cancel V2 and t from both sides:
R1(R1+r)2=R2(R2+r)2
Step 7: Cross-Multiplying
Cross-multiplying gives:
R1(R2+r)2=R2(R1+r)2
Step 8: Expanding Both Sides
Expanding both sides:
R1(R22+2R2r+r2)=R2(R21+2R1r+r2)
This simplifies to:
R1R22+2R1R2r+R1r2=R2R21+2R2R1r+R2r2
Step 9: Rearranging the Equation
Rearranging gives:
R1R22−R2R21+(2R1R2−2R2R1)r+(R1−R2)r2=0
This simplifies to:
R1R2(R2−R1)+(R1−R2)r2=0
Step 10: Factoring Out Common Terms
Factoring out (R1−R2):
(R1−R2)(r2+R1R2)=0
Since R1≠R2, we can divide by (R1−R2):
r2=R1R2
Step 11: Finding the Internal Resistance
Taking the square root gives:
r=√R1R2
Final Answer
The internal resistance of the cell is:
r=√R1R2
We have a cell that sends a current through two different resistances R1 and R2 for the same amount of time t. The heat generated in both resistances is the same. We need to find the internal resistance r of the cell.
The heat developed H in a resistor when a current I flows through it for time t is given by:
H=I2Rt
where R is the resistance.
The current I flowing through a resistor connected to a cell with voltage V and internal resistance r can be expressed as:
I=VR+r
where R is the external resistance.
For the first resistance R1:
H1=I21R1t=(VR1+r)2R1t
For the second resistance R2:
H2=I22R2t=(VR2+r)2R2t
Since the heat developed in both resistances is the same:
H1=H2
This gives us:
(VR1+r)2R1t=(VR2+r)2R2t
We can cancel V2 and t from both sides:
R1(R1+r)2=R2(R2+r)2
Cross-multiplying gives:
R1(R2+r)2=R2(R1+r)2
Expanding both sides:
R1(R22+2R2r+r2)=R2(R21+2R1r+r2)
This simplifies to:
R1R22+2R1R2r+R1r2=R2R21+2R2R1r+R2r2
Rearranging gives:
R1R22−R2R21+(2R1R2−2R2R1)r+(R1−R2)r2=0
This simplifies to:
R1R2(R2−R1)+(R1−R2)r2=0
Factoring out (R1−R2):
(R1−R2)(r2+R1R2)=0
Since R1≠R2, we can divide by (R1−R2):
r2=R1R2
Taking the square root gives:
r=√R1R2
The internal resistance of the cell is:
r=√R1R2
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Match the columns
Explore 4 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Subjective
Explore 11 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Medical entrances gallery
Explore 25 Videos
Similar Questions
A cell supplies a current i1 trhough a resistnace R1 and a current i2 through a resistance R2. The internal resistance of this cell is
View SolutionA cell of emf E and internal resistance r supplies currents for the same time t through external resistances R1=100ΩandR2=40Ω separately. If the heat developed in both cases is the same, then the internal resistance of the cell is
View Solution
Knowledge Check
When a current I flows through a resistance R for time t, the electrical energy spent is :
AIRtBI2RtCIR2tDI2R/t
The terminal voltage is E2 when a c urrent of 2A is flowing through 2Ω resistance, then the internal resistance of cell is:-
View SolutionIn the given circuit, the current through the resistance R is __________ A.
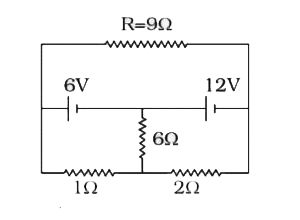
View SolutionA cell develops the same power across two resistances R1 and R2 separately. The internal resistance of the cell is
View SolutionA cell develops the same power across two resistances R1 and R2 separately. The internal resistance of the cell is
View SolutionA cell to emf. E and internal resistance r supplies currents for the same time t through external resistanceR1andR2 respectively. If the heat produced in both cases is the same, then the internal resistance is given by :
View SolutionWhen a celll is connected to an external resistance R1, current through it is i1. When the same cell is connected to an external resistance R2, current through it is i2. Calculate the emf and internal resisance of the cell.
View SolutionThe internal resistance of a 2.1V cell which gives a current 0.2A through a resistance of 10Ω
View Solution

