If a solid A⊕Bɵ having ZnS Structure is heated so that the ions along two of the axis passing throgh the face centre particles are lost and bivalent ion (Z) enters herre to maintain the electrical neutrality, so that the new formula unit becomes AxByZc, report the value of x+y+c.
The correct Answer is:7
To solve the problem, we need to analyze the changes in the solid structure when it is heated and how the introduction of the bivalent ion Z2+ affects the overall composition. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Initial Structure
The solid A+B− has a ZnS structure. In this structure:
- Each unit cell contains 4 A+ ions and 4 B− ions.
- The B− ions are located at the face centers and corners of the unit cell.
Step 2: Identify the Loss of Ions
When the solid is heated, ions along two of the axes passing through the face center particles are lost. This means:
- 2 B− ions are removed from the face centers (1 from each of the 2 face centers).
Step 3: Calculate Remaining Ions
After losing 2 B− ions:
- The number of B− ions left = Initial B− ions - Lost B− ions
- Remaining B− ions = 4−2=2
Step 4: Introduce the Bivalent Ion
To maintain electrical neutrality, a bivalent ion Z2+ enters the structure. Since 2 B− ions were lost, we need 1 Z2+ ion to balance the charge:
- The relationship is 2B−=1Z2+.
Step 5: Write the New Formula
The new formula unit is AxByZc. From our calculations:
- x=4 (number of A+ ions remains the same)
- y=2 (remaining B− ions)
- c=1 (number of Z2+ ions)
Step 6: Calculate x+y+c
Now, we sum the values:
x+y+c=4+2+1=7
Final Answer
The value of x+y+c is 7.
---
The solid A+B− has a ZnS structure. In this structure:
- Each unit cell contains 4 A+ ions and 4 B− ions.
- The B− ions are located at the face centers and corners of the unit cell.
When the solid is heated, ions along two of the axes passing through the face center particles are lost. This means:
- 2 B− ions are removed from the face centers (1 from each of the 2 face centers).
After losing 2 B− ions:
- The number of B− ions left = Initial B− ions - Lost B− ions
- Remaining B− ions = 4−2=2
To maintain electrical neutrality, a bivalent ion Z2+ enters the structure. Since 2 B− ions were lost, we need 1 Z2+ ion to balance the charge:
- The relationship is 2B−=1Z2+.
The new formula unit is AxByZc. From our calculations:
- x=4 (number of A+ ions remains the same)
- y=2 (remaining B− ions)
- c=1 (number of Z2+ ions)
Now, we sum the values:
x+y+c=4+2+1=7
The value of x+y+c is 7.
Topper's Solved these Questions
- SOLID STATEBook:CENGAGE CHEMISTRY ENGLISHChapter:SOLID STATEExercise:Exercises (Fill In The Blanks)
Explore 15 Videos
- SOLID STATEBook:CENGAGE CHEMISTRY ENGLISHChapter:SOLID STATEExercise:Exercises (True/False)
Explore 19 Videos
- SOLID STATEBook:CENGAGE CHEMISTRY ENGLISHChapter:SOLID STATEExercise:Exercises (Assertion-Reasoning)
Explore 19 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBook:CENGAGE CHEMISTRY ENGLISHChapter:REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSExercise:SUBJECTIVE TYPE
Explore 4 Videos
- SOLUTIONSBook:CENGAGE CHEMISTRY ENGLISHChapter:SOLUTIONSExercise:Ex 2.3 (Objective)
Explore 9 Videos
Similar Questions
In a compound oxide ions are arranged in cubic close packing arrangement. Cations A occupy one-sixth of the tetrahedral voids and cations B occupy one-third of the octahdral voids. The formual of the compound is Ax,By,Oz then find the value of x+y+z
View SolutionA spinal is an important class of oxides consisting of two types of metal ions with oxides ions arranged in CCP layer. The normal spinal has one-eighth of the tetrahedral holes occupied by one type of metal ion and one-half of the octahedral holes occupied by another type of metal ion. such a spinal is formed by Zn2+,Al3+andO2− in the tetrahedral holes. if formula of the compound is ZnxAlyOz, then find the value of (x+y+z) ?
View SolutionA solid has a structure in which X atoms are located at cubic corners of unit cell, O atom are at the edge centres and Y atoms at cube centre.
Then the formula of compound is XaYbOc
If two atoms of O missing from any of two edge centres per unit cell, then the molecular formula is XaYbOz. Then, find the value of (x+y+z)−(a+b+c).
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0andx=a. Beyond the line x=a (i.e., in the region x>a), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line x=a.
b. the pitch of the helix formed after the particle enters the region x≥a. (Mass of the particle is m.)
View SolutionA tetrahedron is three dimensional figure bounded by four non coplanar triangular plane. So a tetrahedron has points A,B,C,D as its vertices, which have coordinates (x1,y1,z1)(x2,y2,z2),(x3,y3,z3)and(x4,y4,z4) respectively in a rectangular three –dimensional space. Then the coordinates of its centroid are
(x1+x2+x3+x44,y1+y2+y3+y44,z1+z2+z3+z44).
The circumcentre of the tetrahedron is the centre of a sphere passing through its vertices. So, the circumcentre is a point equidistant from each of the vertices of tetrahedron.
Let tetrahedron has three of its vertices represented by the points
(0,0,0),(6,−5,−1)and(−4,1,3) and its centroid lies at the point (1,−2,5). Now answer the following questions
The distance between the planes x+2y−3z−4=0and2x+4y−6z=1 along the line x1=y−3=z2 is :
View SolutionA compound formed by elements X and Y has a cubic structure in which X atoms are at the corner of the cube and Y atoms are at the face centres. One atoms X is misssing from the corner.
a. Calculate (i). Zeff' (ii). total number of the atoms in the cube, and (iii). formula of the compound.
b. If alll the atoms are removed from one of the faces of the cube containing atoms at corners, as in (a) above, calculate (i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.
View SolutionA tetrahedron is three dimensional figure bounded by four non coplanar triangular plane. So a tetrahedron has points A,B,C,D as its vertices, which have coordinates (x1,y1,z1)(x2,y2,z2),(x3,y3,z3)and(x4,y4,z4) respectively in a rectangular three –dimensional space. Then the coordinates of its centroid are
(x1+x2+x3+x44,y1+y2+y3+y44,z1+z2+z3+z44).
The circumcentre of the tetrahedron is the centre of a sphere passing through its vertices. So, the circumcentre is a point equidistant from each of the vertices of tetrahedron.
Let tetrahedron has three of its vertices represented by the points
(0,0,0),(6,−5,−1)and(−4,1,3) and its centroid lies at the point (1,−2,5). Now answer the following questions
The coordinate of the fourth vertex of the tetrahedron is :
View SolutionA tetrahedron is three dimensional figure bounded by four non coplanar triangular plane. So a tetrahedron has points A,B,C,D as its vertices, which have coordinates (x1,y1,z1)(x2,y2,z2),(x3,y3,z3)and(x4,y4,z4) respectively in a rectangular three –dimensional space. Then the coordinates of its centroid are
(x1+x2+x3+x44,y1+y2+y3+y44,z1+z2+z3+z44).
The circumcentre of the tetrahedron is the centre of a sphere passing through its vertices. So, the circumcentre is a point equidistant from each of the vertices of tetrahedron.
Let tetrahedron has three of its vertices represented by the points
(0,0,0),(6,−5,−1)and(−4,1,3) and its centroid lies at the point (1,−2,5). Now answer the following questions
The equation of the triangular plane of tetrahedron that contains the given vertices is :
View SolutionA compound formed by elements X and Y has a cubic structure in which X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body centre and at the edge centre of the cube.
a. Celculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
b. If all the atoms are removed from one of the body diagonals of the cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
c. If all the atoms from the diagonals of the one of the face of the cube are removed, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
d. If all the atoms are removed from one of the plane passing through the middle of t he cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
e. If all the atoms are removed from one of the axes passing through one of the face centres of the cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
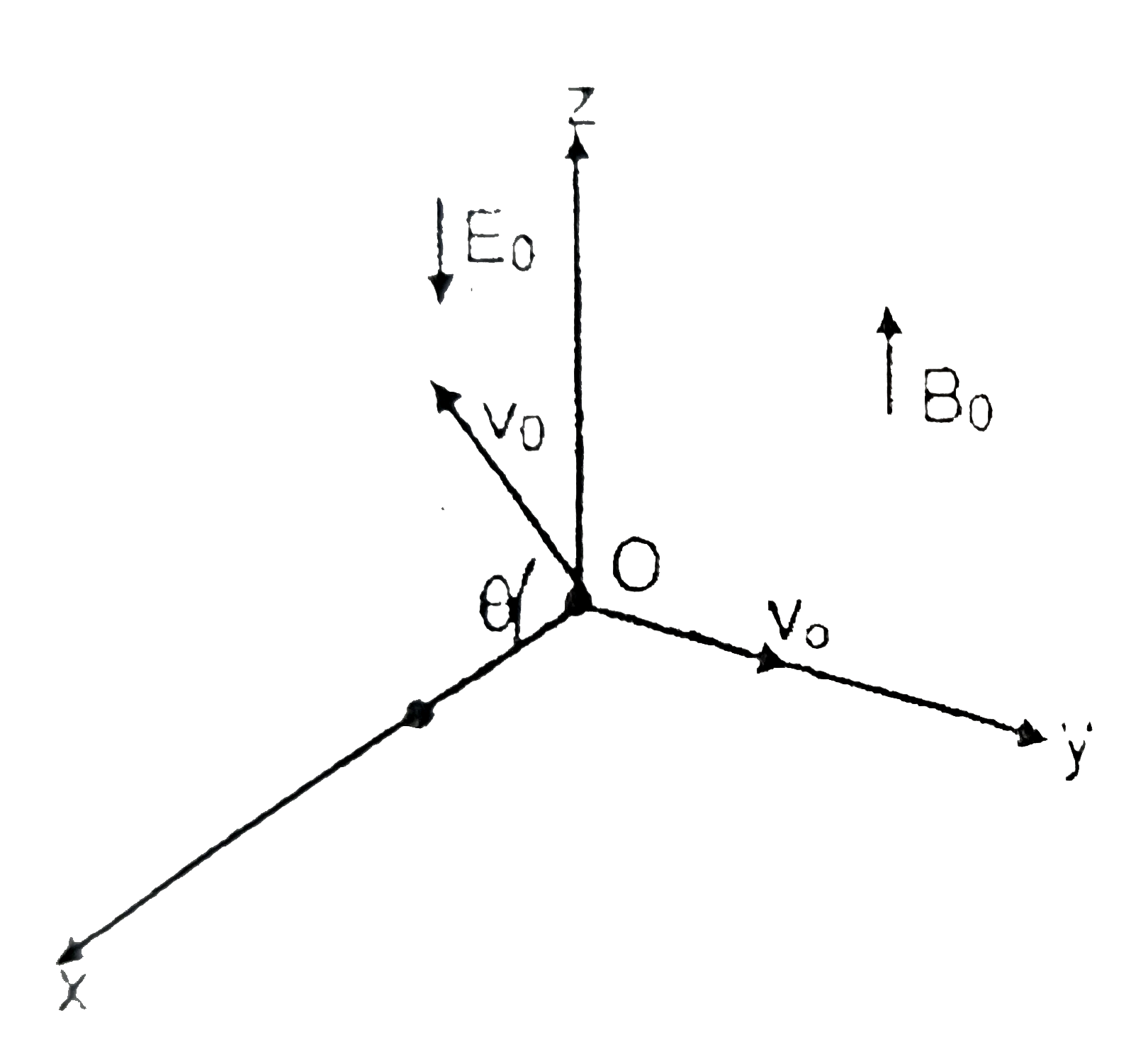
View SolutionA charged point particle having positive charge q, mass m is projected in x−z plane with a speed v0 at an angle θ with the x−axis , while another identical particle is projected simultaneously along the y−axis from the origin (see figure) with an equal speed v0.
An electric field →E=−E0ˆk exists in the x−z plane, while a magnetic field →B=B0ˆk exists in the region y>0 (F0, B0>0). It is observed that both the particles collide after some time. Assume that the space is gravity free.
(i) Find the time after which the particles collide and the coordinates of the point of collision.
(ii) Find the velocity v0 and the angle θ in terms of the other variables.
(iii) What is the maximum value of the z− coordinate of the first particle ?
View Solution

