Calculate the efficiency of packing in case of a metal crystal for
(i) simple cubic
(ii) body-centred cubic
(iii) face-centred cubic (with the assumptions that atoms are touching each other).

Text Solution

Verified by Experts

(i) Simple cubic :
Number of spheres in a unit cell $= 8 \times \frac{1}{8} = 1$
Volume of the sphere $= \frac{4}{3} π r^{3} (r is the radius of the sphere)$
Volume of the cube $= a^{3} = {(2 r)}^{3} = 8 r^{3}$
Effciency of packing $= \frac{4 / 3 π r^{3}}{8 r^{3}} = \frac{π}{6} = 0.524 or 52.4 %$ .
(ii) Body - centred cubic structure :
Assuming that body centre touches the spheres at the corner.
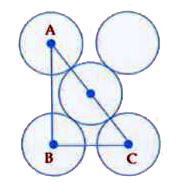
Body diagonal AD = 4r
Face diagonal $A C = \sqrt{A B^{2} + B C^{2}} = \sqrt{a^{2} + a^{2}} = \sqrt{2} a$
Body diagonal $A D = \sqrt{A C^{2} + C D^{2}} = \sqrt{2 a^{2} + a^{2}} = \sqrt{3} a$
$\sqrt{3} a = 4 r or a = \frac{4 r}{\sqrt{3}}$ ,
Volume of unit cell $= a^{3} = {(\frac{4 r}{\sqrt{3}})}^{3} = \frac{64 r^{3}}{3 \sqrt{3}}$

Number of spheres in unit cell $= 8 \times \frac{1}{8} + 1 = 2$
Volume of two spheres $= 2 \times \frac{4}{3} π r^{3} = \frac{8}{3} π r^{3}$
Efficiency of packing $= \frac{8 π r^{3} / 3}{64 r^{3} / 3 \sqrt{3}} = \frac{π \sqrt{3}}{8} = 0.68 or 68 %$
(iii) Face - centred cubic :
$A C = \sqrt{A B^{2} + B C^{2}} = \sqrt{a^{2} + a^{2}} = \sqrt{2} a$
$∴ \sqrt{2} a = 4 r or a = \frac{4}{\sqrt{2}} \times r$
Volume of the unit cell $= a^{3} = \frac{32}{\sqrt{2}} r^{3}$
Number of sphere in a unit cell $= 8 \times \frac{1}{8} + 6 \times \frac{1}{2} = 4$
Volume of four spehres $= 4 \times \frac{4}{3} π r^{3} = \frac{16}{3} π r^{3}$
Efficiency of packing $= \frac{16 π r^{3} / 3}{32 r^{3} / \sqrt{2}} = 0.74 or 74 %$ .

Calculate the efficiency of packing in case of metal crystal for simple cubic (with the assumption that atoms are touching each other.
A0.524
B0.624
C0.544
D0.724
In a simple cubic, body-centred cubic and face-centred cubic structure, the ratio of the number of atoms present is respectively
A8:1:6
B1:2:4
C4:2:1
D4:2:3