The complex number z1,z2andz3 satisfying z1−z3z2−z3=1−i√32 are the vertices of a triangle which is :
of area zero
right-angled isosceles
equilateral
obtuse-angled isosceles
The correct Answer is:C
We have,
z1−z3z2−z3=1−i√32
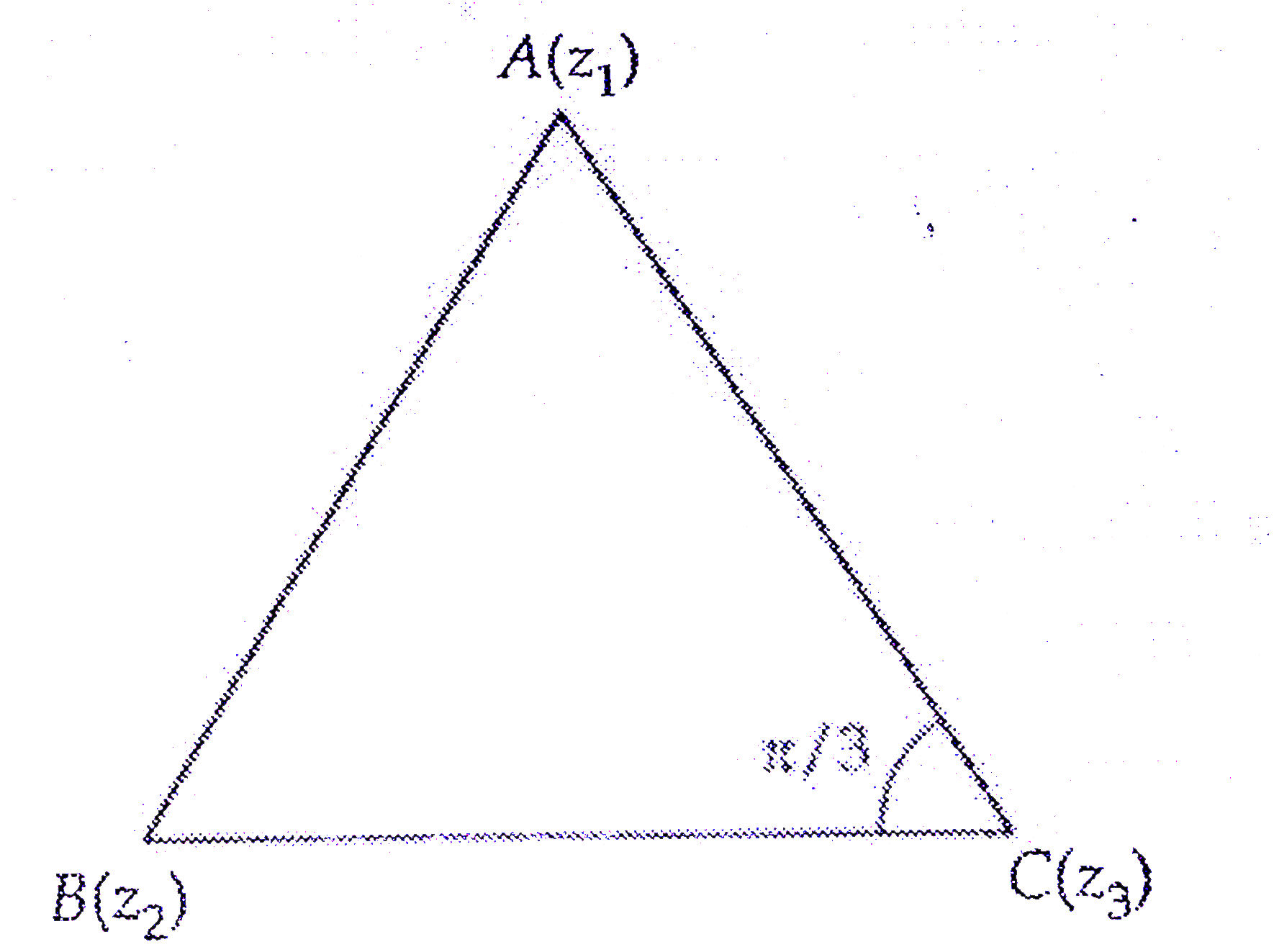
⇒(z1−z3)=e−π/3(z2−z3).
⇒¯¯¯¯¯¯CA is obtained by rotating ¯¯¯¯¯¯CB through π/3 in clockwise sense.
⇒ CA=CB and ∠AOB=π3
⇒△ABC is an equilateral triangle.
Topper's Solved these Questions
- COMPLEX NUMBERS Book:OBJECTIVE RD SHARMAChapter:COMPLEX NUMBERS Exercise:Section II - Assertion Reason Type
Explore 15 Videos
- COMPLEX NUMBERS Book:OBJECTIVE RD SHARMAChapter:COMPLEX NUMBERS Exercise:Exercise
Explore 131 Videos
- COMPLEX NUMBERS Book:OBJECTIVE RD SHARMAChapter:COMPLEX NUMBERS Exercise:Chapter Test
Explore 59 Videos
- CIRCLESBook:OBJECTIVE RD SHARMAChapter:CIRCLESExercise:Chapter Test
Explore 55 Videos
- CONTINUITY AND DIFFERENTIABILITYBook:OBJECTIVE RD SHARMAChapter:CONTINUITY AND DIFFERENTIABILITYExercise:Exercise
Explore 86 Videos
Similar Questions
The complex numbers z1z2andz3 satisfying z1−z3z2−z3=1−i√32 are the vertices of triangle which is (1) of area zero (2) right angled isosceles(3) equilateral (4) obtuse angled isosceles
View SolutionThe complex number z1,z2andz3 satisfying z1−z3z2−z3=1−i√32 are the vertices of a triangle which is :
View Solution
Knowledge Check
Complex number z1,z2andz3 in AP
Alie on ellipseBlie on a parabolaClie on lineDlie on circleThe complex number z1,z2andz3 satisfying z1−z3z2−z3=1−i√32 are the vertices of a triangle which is :
Aof area zeroBright - angled isoscelesCequilateralDobtuse - angled isoscelesThe complex numbers z1,z2,z3 stisfying (z2=z3)=(1+i)(z1−z3).wherei=√−1, are vertices of a triangle which is
AequilateralBisoscelesCright angledDscalene
For complex numbers z1=6+3i,z2=3−I find z1z2
View SolutionLet z1,z2andz3 be three complex numbers such that z1+z2+z3=z1z2+z2z3+z1z3=z1z2z3=1. Then the area of triangle formed by points A(z1),B(z2)andC(z3) in complex plane is _______.
View SolutionThe complex number z satisfying |z−1|=|z−3|=|z−i| is
View SolutionThe complex number z =x+iy which satisfies the equation ∣∣∣z−3iz+3i∣∣∣=1, then on
View SolutionThe complex numbers z1,z2,z3 are the vertices of a triangle . Then the complex numbers z which make the triangle into a parallelogram is
View Solution

