Let ABCD be a square and let P be a point on AB such that AP:PB=1:2.if∠APD=θ, then what is the value of cosθ?
1√10
1√5
2√10
2√5
The correct Answer is:A
To solve the problem, we will follow a systematic approach.
1. Understanding the Problem:
We have a square ABCD and a point P on side AB such that the ratio of lengths AP to PB is 1:2. We need to find the value of cos(θ), where θ is the angle APD.
2. Assigning Lengths:
Let the length of side AB (and all sides of the square) be denoted as X. Given the ratio AP:PB = 1:2, we can express the lengths as:
- AP = X3
- PB = 2X3
3. Identifying Points:
Place the square in the coordinate system:
- A(0, 0)
- B(X, 0)
- C(X, X)
- D(0, X)
- P will be at (AP, 0) = (X3,0)
4. Finding the Lengths:
Now, we need to find the length DP. The coordinates of D are (0, X) and P are (X3,0).
Using the distance formula:
DP=√(0−X3)2+(X−0)2
DP=√(X3)2+X2=√X29+X2=√X29+9X29=√10X29=X√103
5. Using Cosine Definition:
We know that cos(θ) is defined as the adjacent side over the hypotenuse in the right triangle ADP:
cos(θ)=APDP
Substituting the values we found:
cos(θ)=X3X√103=1√10
6. Final Answer:
Thus, the value of cos(θ) is:
cos(θ)=1√10
Conclusion:
The final answer is:
cos(θ)=1√10
We have a square ABCD and a point P on side AB such that the ratio of lengths AP to PB is 1:2. We need to find the value of cos(θ), where θ is the angle APD.
Let the length of side AB (and all sides of the square) be denoted as X. Given the ratio AP:PB = 1:2, we can express the lengths as:
- AP = X3
- PB = 2X3
Place the square in the coordinate system:
- A(0, 0)
- B(X, 0)
- C(X, X)
- D(0, X)
- P will be at (AP, 0) = (X3,0)
Now, we need to find the length DP. The coordinates of D are (0, X) and P are (X3,0).
Using the distance formula:
DP=√(0−X3)2+(X−0)2
DP=√(X3)2+X2=√X29+X2=√X29+9X29=√10X29=X√103
We know that cos(θ) is defined as the adjacent side over the hypotenuse in the right triangle ADP:
cos(θ)=APDP
Substituting the values we found:
cos(θ)=X3X√103=1√10
Thus, the value of cos(θ) is:
cos(θ)=1√10
The final answer is:
cos(θ)=1√10
Topper's Solved these Questions
Similar Questions
ABCD is square. K and L are two points on AB such that AO = AK and BO = BL and ∠LOK=θ.
Find the value of tanθ.
View SolutionIn the given figure, ABCD is a parallelogram. Point P is at BC such that PB : PC = 1 : 2. The extended DP and extended AB meets at point Q. If the area of BPQ is 20 unit2 then find the area of ΔDCP.
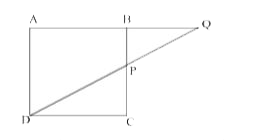
View Solution
Knowledge Check
Let ABCD be a square and let P be point on segment CD such that DP : PC = 1 : 2. Let Q be a point on segment AP such that ∠BQP=90∘. Then the ratio of the area of quadrilateral PQBC to the area of the square ABCD is
A3160B3760C3960D4160ABCD is a square , E is a point on AB such that BE=17 cm. The area of triangle ADE is 84 cm2 . What is the area of square ?
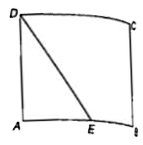 A400cm2B625cm2C729cm2D576cm2
A400cm2B625cm2C729cm2D576cm2ABCD is a parallelogram. If P be a point on CD such that AP=AD , then the measure of ∠PAB+∠BCD is:
A180∘B225∘C240∘D135∘
A rod of AB of length 3 rests on a wall as follows :
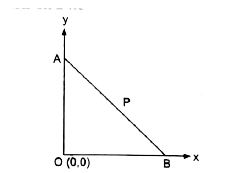
P is a point on AB such that AP:PB=1:2 If the rod slides along the wall, then the locus of P lies on
View SolutionIn the given figure, ABCD is a square and P is a point inside it such that PB=PD. Prove that CPA is a straight line.
View SolutionLet ABCD be a convex quadrilateral with perpendicular diagonals. If AB=20, BC=70 and CD=90, then what is the value of DA?
View SolutionA rod of AB of length 3 rests on a wall as follows :

P is a point on AB such that AP:PB=1:2 If the rod slides along the wall, then the locus of P lies on
View SolutionLet a vertical tower AB have its end A on the level ground. Let C be the mid-point of AB and P be a point on the ground such that AP = 2AB. If √BPC=β, then tan β is equal to
View Solution

