Question

Method Of Integration

Explanation

Methods of Integration, Application  & Techniques

Doubtnut presents interactive Methods of Integration in Maths. In the video tutorials, our experts have shared the simplest mathematical tricks and approaches towards integrating some troublesome functions. All video tutorials on Doubtnut are FREE. All you need is an internet connection to play videos for learning Integration Physics with Doubtnut.

Let us first understand, what is Integration in Mathematics? before getting started with learning various types of integration methods.

What is Integration in Mathematics?

Integration can be learned as the reverse of Differentiation, the rate of change of a function. The process of finding a function, whose derivatives are already given, is called anti-differentiation i.e. Integration. If F'(x) = f(x), we say F(x) is an anti-derivative of f(x).

Symbol of Integration

The symbol for integration is an S-shaped integral sign “∫,” as in ∫ f(x), usually called the indefinite integral of the function.

Constant of Integration

The constant of integration is represented by the constant, C; it expresses a sense of uncertainty. For an assumed derivative, there can be numerous integrands that may differ by a set of real numbers. This set of real numbers is known as the constant of Integration.

Example of Integration

F(x) =cos x is an anti-derivative of sin x

And, e^x is an anti-derivative of e^x.

Note:

If F(x) is an anti-derivative of f(x) 

Then,

F(x) + c, here c, as said earlier is the constant of integration. This is because the derivative of a constant function is 0. As a matter fact, they basically the anti-derivatives of f(x).

Here is a pictorial description for easy understanding

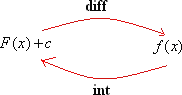
We write,

f(x) dx  = F (x) + c.

If F'(x) = f(x).

It is known as the indefinite integral of f(x).

Therefore, to find the indefinite integral of a function, you need to be already familiar with the different techniques of differentiation in Mathematics.

Application of Integration

The techniques of Integration can be utilized to find out the areas, volumes or even the center points. In primary classes, we have learned how to find area or volume of shapes with fixed straight lines i.e. area of a circle, the volume of a cylinder or area of a triangle. But, how do we calculate the area or volume of an object with irregular or curved edges? Methods of Integration are helpful in such cases.

Listed below are some applications of Method of Integration:

1. To find displacement and velocity using the indefinite integral


2. To find the area under a curve


3. To find the area between the two curves


4. To find the volume of an object with curved sides, for instance, wine barrels


5. To find out the center point of an area with curved sides

Integration Techniques

There are two basic types of Integrals:

1. Indefinite Integrals: It is an integral of a function when there is no limit for integration. It contains an arbitrary constant.


2. Definite Integrals: An integral of a function with limits of integration. There are two values as the limits for the interval of integration. One is the lower limit and the other is the upper limit. It does not contain any constant of integration.

In integration, we already have a derivative of a function, for which we need to find the integrands. Basically, integration is the inverse process of differentiation.

Tabulated below is the derivative function and there subsequent integrals or anti-derivatives:

Derivatives	Integrals
d⁄dx (x n + 1 ⁄ n + 1) = xn	∫ xn dx = x n + 1 ⁄ (n + 1) + C, n ≠ −1
d ⁄ dx (x) = 1	∫dx = x + C
d⁄dx (sin x) = cos x	∫ cos x dx = sin x + C
d ⁄ dx (− cos x) = sin x	∫sinx dx = − cos x + C
d⁄dx (tan x) = sec 2 x	∫ sec 2 x dx = tan x + C
d ⁄ dx (− cot x) = cosec 2 x	∫ cosec 2 x dx = − cot x+ C
d ⁄ dx (sec x) = sec x tan x	∫(sec x + tan x)dx = sec x + C
d⁄dx (− cosec x) = cosec x cot x	∫(cosec x cot x)dx = − cosec x + C
d ⁄ dx (sin−1 x) = 1⁄ √(1 − x2)	∫ dx ⁄ √(1 − x2) = sin−1 x+ C
d⁄dx (− cos−1 x) = 1⁄ √(1 − x2)	∫dx ⁄ √(1 − x2) = − cos−1 x + C
d ⁄ dx (tan−1 x) = 1⁄ (1 + x2)	∫ dx ⁄ (1 + x2) =tan−1 x + C
d⁄dx (− cot−1 x) = 1⁄ (1 + x2)	∫dx  ⁄ (1 + x2) = − cot−1 x + C
d ⁄ dx (sec−1 x)  = 1⁄ x√(x2 − 1)	∫ dx ⁄ x√(x2 − 1) = sec−1 x + C
d⁄dx (− cosec−1 x)  = 1⁄ x√(x2 − 1)	∫dx ⁄ x√(x2 − 1) = − cosec−1 x + C
d⁄dx (log |x|) = 1⁄x	∫1⁄x dx = log |x| + C

Methods of Integration

Method of integration holds paramount importance in the CBSE board exam Maths syllabus as well as competitive examination. In school-based exams, the Minimum 4-6 marks question is expected from this section. Therefore, students must invest time and energy learning various Methods of Integration given below.

The different methods of integration include:

Integration by Substitution:

As per the substitution method, a given integration function ∫ f(x) dx can be converted into another form by altering the independent variable x to t. It is done by substituting x = g (t).

Consider, I = ∫ f(x) dx

Now, substitute x = g(t) so that, dx/dt = g’(t) or dx = g’(t)dt.

Therefore, I = ∫ f(x) dx = ∫ f[g(t)] g’(t)dt

NCERT Example for Practice: Integrate sin (mx) with respect to x.

Solution: We know that the derivative of mx = m.

Hence, let’s substitute mx = t,

so that mdx = dt.

Therefore, ∫ sin mx dx

= 1/m ∫ sin t dt

= – 1/m cos t + C

= – 1/m cos mx + C

Integration Using Trigonometric Identities

To integrate a function, if the integrand encompasses any kind of trigonometric function, then the trigonometric identities can be utilized to simplify the function. It can be easily integrated.

Listed below are some trigonometric identities:

1. sin²x = 1−cos2x / 2


2. cos² = 1+cos2x / 2


3. sin³x = 3 sinx–sin3x / 4


4. cos³x = 3cosx+cos3x / 4

All these identities simplify integrand, which can be easily calculated.

Integration of Some particular function

Integration of some particular function implicates some imperative formulae of integration which can be operated to make other integration into the typical form of the integrand. The integration of these integrands can be easily evaluated using a direct form of integration method.

Integration by partial fraction

As we know, Rational Number are expressed in the form of p/q,

Here, p and q are integers and q≠0.

Similarly,

A rational function is defined as the ratio of two polynomials which can be expressed in the form of partial fractions: P(x)/Q(x),

Where, Q(x)≠0.

There are two forms of partial fraction:

1. Proper partial fraction: If the power of the numerator is less than to that of the denominator, then it is a proper fraction.


2. Improper partial fraction: When the power of the numerator is greater than to that of denominator then it is known as an improper fraction. Therefore, the fraction can be simplified and can be easily integrated.

Integration by Parts

The integration by parts in calculus is a special method of integrating two functions when they are multiplied.

Arithmetically, Integration by parts is given as-

∫f(x).g(x)dx=f(x)∫g(x)dx−∫f′(x).(∫g(x)dx)dx

ILATE: It helps in identification of a function that comes first on the given list and selects it as f(x).

ILATE stands for-

• I: Inverse trigonometric functions i.e. arctan x, arcsec x, arcsin x etc.


• L: Logarithmic functions i.e. ln x, log5(x), etc.


• A: Algebraic functions


• T: Trigonometric functions i.e. sinx, cosx , tan x etc .


• E: Exponential functions

Here is an NCERT example for your better understanding and practice:

Calculate: ∫ x.exdx

Answer:

From aforementioned ILATE theorem, f(x) = x, and g(x) = e²

Thus applying the method of integration by parts, we get

∫f(x).g(x)dx=f(x)∫g(x)dx−∫f′(x).(∫g(x)dx)dx

∫x.e^xdx = x.∫e^xdx–∫1.(∫e^xdx)dx

= x.e^x–e^x+c

Hence Proved!