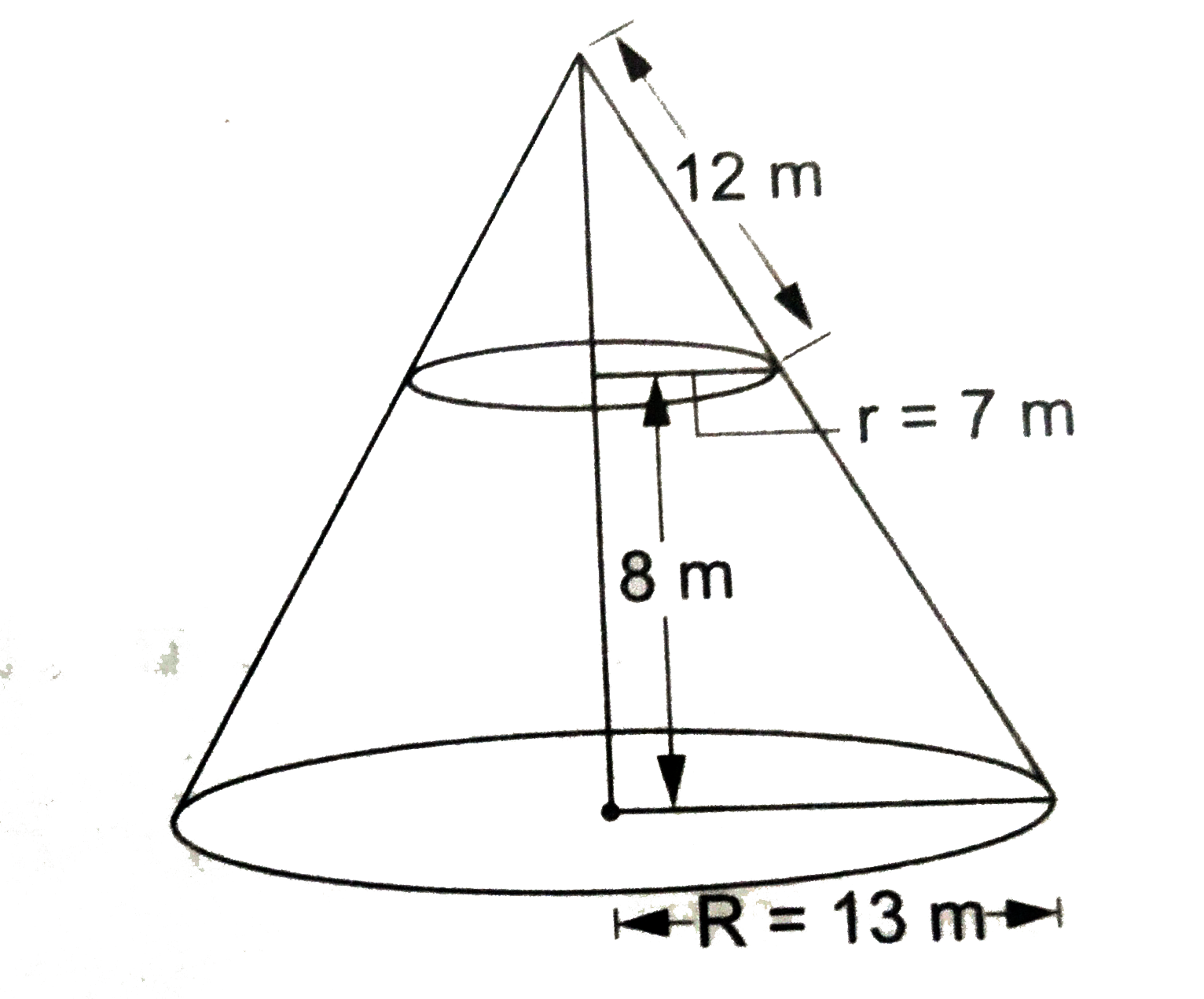
A tent consists of a frustum of a cone, surmounted by a cone. If the diameters of the upper and lower and circular ends of the frustum be 14 m and 26 m respectively, the height of the frustum be 8 m and the slant height of the surmounted conical portion be 12 m, find the area of the canvas required to make the tent. (Assume that the radii of the upper circular end of the frustum and the base of the surmounted conical portion are equal).

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $892.6 m^{2}$

$R = 12 m, r = 7 m and h = 8 m$ ,
$∴ l = \sqrt{h^{2} + {(R - 0 r)}^{2}} = 10 m$ .
Required area
$= {\frac{22}{7} \times 10 \times (13 + 7) + \frac{22}{7} \times 7 \times 12} m^{2}$

|

Updated on:21/07/2023

Class 10 MATHS SURFACE AREAS AND VOLUMES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A circus tent is cylindrical to a height of 3 meters and conical above it. If the radius of the base is 52.5 m and the slant height of the cone is 52 m,then the total area of the canvas required to make it is:
A3048 $π$
B $3045 π$
C $2730 π$
D $2842 π$
Question 2 - Select One
A frustum of a cone has height 8 cm and radii of upper and lower circular surfaces are 22 cm and 16 cm respecticely. Its slant height is
A10 cm
B $8 \sqrt{5}$ cm
C $4 \sqrt{6}$ cm
D $6 \sqrt{3}$ cm
Question 3 - Select One
A circus tent is cylindrical up to a height of 3m and conical above it. If its diameter is 105m and the slant height of the conical part is 63 m, then the total area of the canvas required to make the tent is (take $π = \frac{22}{7}$ )
A $11385 m^{2}$
B $10395 m^{2}$
C $9900 m^{2}$
D $990 m^{2}$

RS AGGARWAL-VOLUME AND SURFACE AREAS OF SOLIDS-Exercise 17C

Home
Ask Doubt
Profile