A toy is in the form of a cylinder with hemispherical ends. If the whole length of the toy is 90 cm and its diameter is 42 cm , find the cost of painting the toy at the rate of 70 paise per sq m .
The correct Answer is:Rs.8316
To solve the problem, we will follow these steps:
Step 1: Identify the dimensions of the toy
The toy is in the shape of a cylinder with two hemispherical ends. We know:
- Total length of the toy = 90 cm
- Diameter of the toy = 42 cm
From the diameter, we can find the radius:
- Radius (r) = Diameter / 2 = 42 cm / 2 = 21 cm
Step 2: Calculate the height of the cylindrical part
Since the toy has two hemispherical ends, the total length of the toy includes the height of the cylinder and the diameters of the two hemispheres. The height of the two hemispheres combined is equal to the diameter of the toy:
- Height of the two hemispheres = Diameter = 42 cm
Now, we can find the height of the cylindrical part (H):
- Total length = Height of cylinder + Height of two hemispheres
- 90 cm = H + 42 cm
- H = 90 cm - 42 cm = 48 cm
Step 3: Calculate the curved surface area (CSA) of the cylinder
The formula for the curved surface area of a cylinder is given by:
CSAcylinder=2πrh
Where:
- r = radius of the cylinder = 21 cm
- h = height of the cylinder = 48 cm
Substituting the values:
CSAcylinder=2×227×21×48
Calculating:
CSAcylinder=2×227×21×48=2×22×21×487
=2×220327=440647≈6309.14 cm2
Step 4: Calculate the surface area of the two hemispherical ends
The formula for the surface area of a sphere is:
SAsphere=4πr2
Since we have two hemispheres, the total surface area of the two hemispheres is:
SAhemispheres=2×SAsphere=2×4πr2=8πr2
Substituting the radius:
SAhemispheres=8×227×(21)2
=8×227×441=8×97027=776167≈11023.71 cm2
Step 5: Calculate the total surface area of the toy
Now, we can find the total surface area (TSA) of the toy:
TSA=CSAcylinder+SAhemispheres
=6309.14+11023.71≈17332.85 cm2
Step 6: Convert the total surface area into square meters
Since the cost is given per square meter, we need to convert square centimeters to square meters:
1 m2=10000 cm2
So,
TSA in m2=17332.8510000≈1.733285 m2
Step 7: Calculate the cost of painting the toy
The cost of painting is given as 70 paise per square meter. First, convert paise to rupees:
70 paise=0.70 rupees
Now, calculate the total cost:
Cost=TSA in m2×Cost per m2
=1.733285×0.70≈1.2133 rupees
Final Answer
The cost of painting the toy is approximately ₹1.21.
The toy is in the shape of a cylinder with two hemispherical ends. We know:
- Total length of the toy = 90 cm
- Diameter of the toy = 42 cm
- Radius (r) = Diameter / 2 = 42 cm / 2 = 21 cm
Since the toy has two hemispherical ends, the total length of the toy includes the height of the cylinder and the diameters of the two hemispheres. The height of the two hemispheres combined is equal to the diameter of the toy:
- Height of the two hemispheres = Diameter = 42 cm
- Total length = Height of cylinder + Height of two hemispheres
- 90 cm = H + 42 cm
- H = 90 cm - 42 cm = 48 cm
The formula for the curved surface area of a cylinder is given by:
CSAcylinder=2πrh
Where:
- r = radius of the cylinder = 21 cm
- h = height of the cylinder = 48 cm
CSAcylinder=2×227×21×48
CSAcylinder=2×227×21×48=2×22×21×487
=2×220327=440647≈6309.14 cm2
The formula for the surface area of a sphere is:
SAsphere=4πr2
Since we have two hemispheres, the total surface area of the two hemispheres is:
SAhemispheres=2×SAsphere=2×4πr2=8πr2
SAhemispheres=8×227×(21)2
=8×227×441=8×97027=776167≈11023.71 cm2
Now, we can find the total surface area (TSA) of the toy:
TSA=CSAcylinder+SAhemispheres
=6309.14+11023.71≈17332.85 cm2
Since the cost is given per square meter, we need to convert square centimeters to square meters:
1 m2=10000 cm2
So,
TSA in m2=17332.8510000≈1.733285 m2
The cost of painting is given as 70 paise per square meter. First, convert paise to rupees:
70 paise=0.70 rupees
Cost=TSA in m2×Cost per m2
=1.733285×0.70≈1.2133 rupees
The cost of painting the toy is approximately ₹1.21.
Topper's Solved these Questions
- VOLUME AND SURFACE AREAS OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREAS OF SOLIDSEXERCISE - EXERCISE 17 A
4 Videos
- VOLUME AND SURFACE AREAS OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREAS OF SOLIDSEXERCISE - Exercise 17B
35 Videos
- VOLUME AND SURFACE AREAS OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREAS OF SOLIDSEXERCISE - VOLUME AND SURFACE AREA OF A COMBINATION OF SOLIDS (SOLVED EXAMPLES )
2 Videos
- TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES EXERCISE - Exercise 12
15 Videos
Similar Questions
Combination of cylinder and hemisphere : A solid is in the form of a cylinder with hemispherical ends. The the whole length of the solid is 108 cm and the diameter of the hemispherical ends is 36 cm; Find the cost of polishing the surface of the solids at the rate of 7 paise per sq. cm.
View SolutionA solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each hemispherical end is 7 cm, find the cost of polishing its surface at the rate of Rs 2 per dm2 (takeπ = 22/7)
View SolutionA wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base of the cone is 5cm and its height is 4cm. Find the cost of painting the toy at the rate of Rs. 5 per 1000cm2.
View SolutionA toy is in the shape of a cone mounted on a hemisphere of same base radius. If the volume of the toy is 231 cm3 and its diameter is 7 cm, find the height of the toy
View SolutionThe solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 108cm and the diameter of the hemispherical ends is 36cm, find the cost of polishing the surface of the solid at the rate of 7 paise per sq. cm (Useπ=227)
View SolutionA solid is composed of a cylinder with hemispherical ends.If the whole length of the solid is 104 cm and the readius of each of its hemispherical ends is 7 cm , find the cost of polishing its surface at the rate of ₹ 10 per dm2
View Solution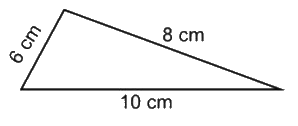
The cost of painting the given sign board at the rate of 9 paise per cm2 is
View SolutionA solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each of the hemispherical ends is 7 cm, find the cost of polishing its surface at the rate of Rs 10 per dm2
View SolutionA solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
View SolutionA solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 20 cm and the diameter of the cylinder is 7 cm. Find the total volume of the solid. (Use F=227)
View Solution
