A right triangle, whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed.

Video Solution

Text Solution

Verified by Experts

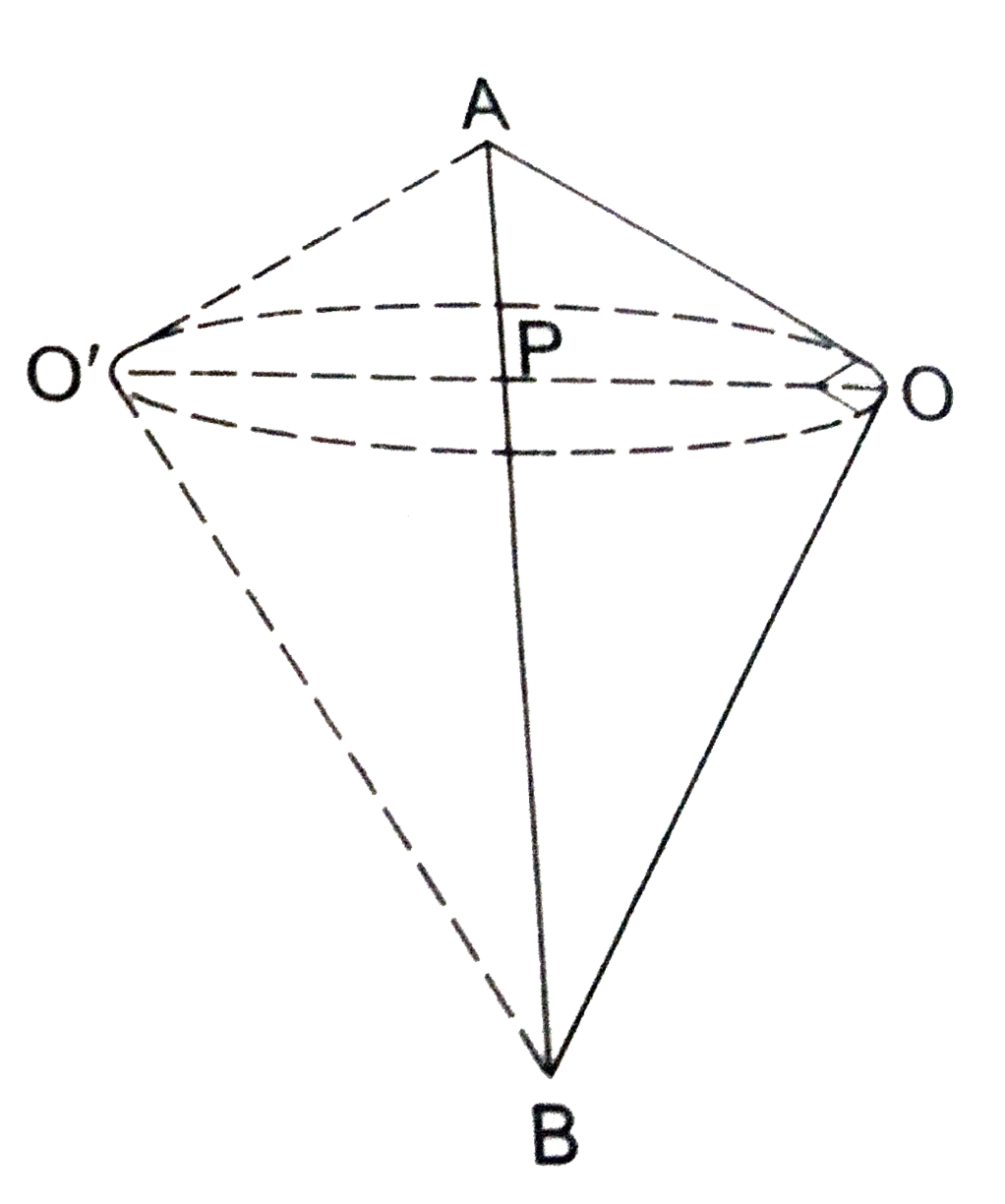
Let $Δ A O B$ be the given right triasngle in which $∠ A O B = 90^{\circ}$ . When $Δ A O B$ is rotated about the hypotenus AB, the two cones generated are AO'O and BO'O.
Clearly, $O A = 3 c m, O B = 4 c m$ .
In right-angled $Δ A O B$ , we have
$A B = \sqrt{{(O A)}^{2} + {(O B)}^{2}} = \sqrt{3^{2} + 4^{2}} c m$
$= \sqrt{25} c m = 5 c m$ .
Let OP = x cm. Then,
$\frac{1}{2} \times O A \times O B = \frac{1}{2} \times A B \times O P$
$\Rightarrow \frac{1}{2} \times 3 \times 4 = \frac{1}{2} \times 5 \times O P \Rightarrow O P = (\frac{3 \times 4}{5}) c m = 2.4 c m .$
In rihgt-angled $Δ A P O$ , we have
$A P = \sqrt{{(O A)}^{2} - {(O P)}^{2}} = \sqrt{3^{2} - {(2.4)}^{2}} c m$
$= \sqrt{9 - 5.76} c m = \sqrt{3.24} c m = 1.8 c m .$
$B P = A B - A P = (5 - 18) c m = 3.2 c m .$
$∴ radius of each of the cones AO'O and BO'O, r = OP = 2.4 cm$
$Height of the coneAO'O, h = AP = 1.8 cm .$
$Height of the cne BOO', H=BP=3.2 cm .$
Volume of the double cone
= volume of the the cone AO'O + volume of the cone BOO'
$\frac{1}{3} π r^{2} h + \frac{1}{3} π r^{2} H = \frac{1}{3} π r^{2} (h + H)$
$= (\frac{1}{3} \times 3.14 \times 2.4 . \times 2.4 \times 5) c m^{3} = 30.144 c m^{3}$ .
Slant height of the cone AO'O, $l_{1} = O A = 3 c m$ .
Slant height of the cone BO'O $l_{2} = O B = 4 c m$ .
Surface area of the double cone
=curved cusrface of the cone AO'O + curved surface area of the cone BOO'
$= π r l_{1} + π r l_{2} + π r l_{2} = π r (l_{1} + l_{1}) = [\frac{22}{7} \times 2.4 \times (3 + 4)] c m^{2}$
$= (\frac{22}{7} \times 2.4 \times 7) c m^{2} = 52.8 c m^{2} .$

Updated on:21/07/2023

|

Class 10 MATHS SURFACE AREAS AND VOLUMES

Topper's Solved these Questions

Similar Questions

RS AGGARWAL-VOLUME AND SURFACE AREAS OF SOLIDS-MULTIPLE-CHOICE QUESTIONS(MCQ)

Home
Ask Doubt
Profile