The decorative block is made of two solids a cube and a hemisphere. The base of the block is a cube with edge 5 cm, and the hemisphere fixed on the top has a diameter of 4.2 cm. Find the total surface area of the block.
The correct Answer is:163.86cm2
Edge of the cube a= 5 cm.
Radius of the hemisphere, r=4.22cm=2.1cm
Total area to be painted
= total surfcae area of the cube - base area of the hemisphere + curved surface area of the hemisphere
=6a2−πr2+2πr2=6a2+πr2
=(6×5×5+227×2.1×2.1)cm2
=(150+13.86)cm2=163.86cm2
(##RSA_MATH_X_C17_S01_024_S01.png" width="80%">
Topper's Solved these Questions
- VOLUME AND SURFACE AREAS OF SOLIDSBook:RS AGGARWALChapter:VOLUME AND SURFACE AREAS OF SOLIDSExercise:VOLUME AND SURFACE AREA OF A COMBINATION OF SOLIDS (SOLVED EXAMPLES )
Explore 2 Videos
- VOLUME AND SURFACE AREAS OF SOLIDSBook:RS AGGARWALChapter:VOLUME AND SURFACE AREAS OF SOLIDSExercise:Exercise 17A
Explore 28 Videos
- TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES Book:RS AGGARWALChapter:TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES Exercise:Exercise 12
Explore 15 Videos
Similar Questions
The decorative block is made of two solids — a cube and a hemisphere. The base of the block is a cube with edge 5 cm, and the hemispherefixed on the top has a diameter of 4.2 cm. Find the total surface area of the block.
View SolutionA decorative block shown in Fig. 16.50 is made of two solids a cube and a hemisphere. The base of the block is a cube with edge 5 cm, and the hemisphere fixed on the top has a diameter 4.2 cm. Find the total surface area of the block (Take π=22/7 ).
View SolutionIn Figure , a decorative block, made up of two solids a cube and a hemisphere . The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has a diameter of 3.5 cm .Find the total surface area of the block ( use π=227)

View SolutionIn Figure a decorative block is shown which is made of two solids , a cube and a hemisphere .The base of the block is cube with edge 6 cm and the hemisphere fixed on the top has a diameter of 4.2 cm .Find :
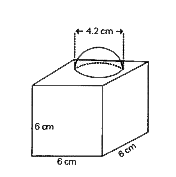
the volume of the block formed
View SolutionThe base of the block is a cube of side 6 cm and the hemisphere fixed on the top has a diameter of 3.5 cm. Find the total surface area of the block. (use π=227)

View SolutionThe radius of a hemisphere is 2.5 cm. Find its total surface area.
View SolutionIf the length of the cube is 6 cm. Then find the total surface area of a cube.
View SolutionThe edge of a cube is 3 cm. Find the total surface area and the volume of the cube.
View SolutionIf the length of the edge of a cube is 3.2 cm, then the total surface area of the cube is
View SolutionFind the total surface area of a cube whose edge is 8 cm.
View Solution
