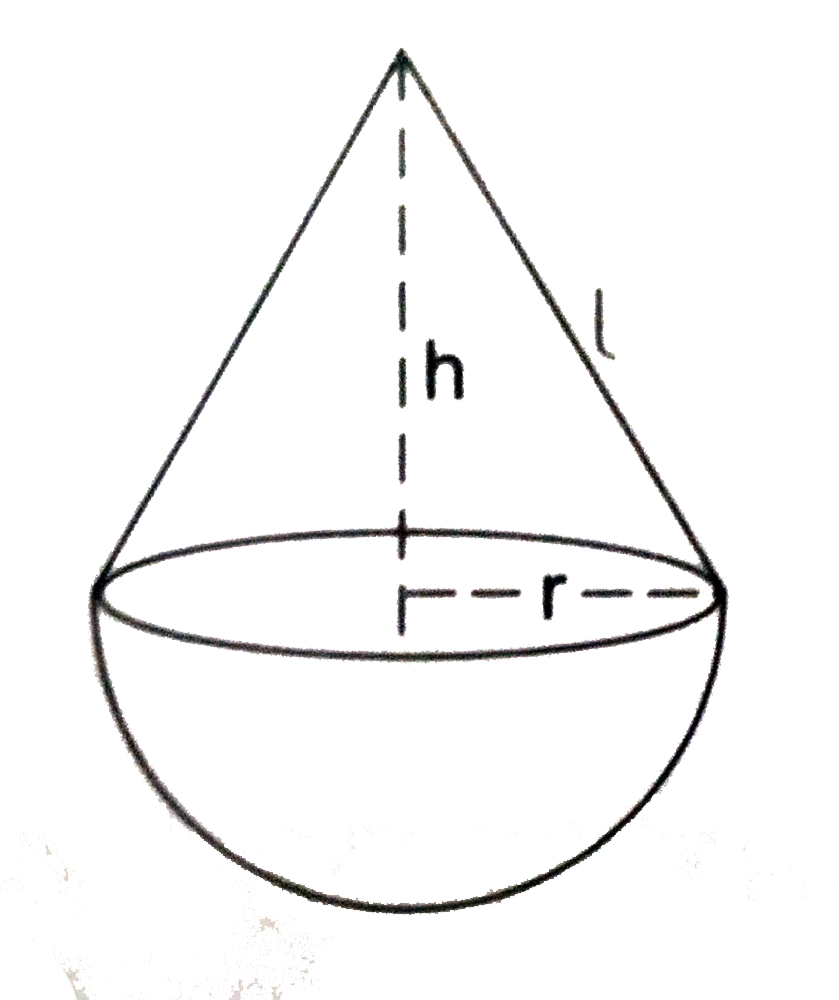
A solid is in the shape of a cone mounted on a hemisphere of same base readius. If the curved surface areas of the hemisphere part and the conical part are equal then find the ratio of the radius and the height of the conical part.

A

$1 : 3$

B

$1 : \sqrt{3}$

C

$1 : 2$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let the radius of each of the cone and the hemisphere be r ,Let the height of the cone be h and its slant height be l.
Then ,curved surface area of the hemsisphere
=curved surface area of the cone
$\Rightarrow 2 π r^{2} = π r l \Rightarrow 2 π r^{2} = π r \sqrt{r^{2} + h^{2}}$
$\Rightarrow = \sqrt{r^{2} + h^{2}} \Rightarrow 4 r^{2} + h^{2}$
[squaring both sides]
$\Rightarrow 3 r^{2} = h^{2} \Rightarrow \frac{r^{2}}{h^{2}} = \frac{1}{3} \Rightarrow \frac{r}{h} = \sqrt{\frac{1}{3}} = \frac{1}{\sqrt{3}}$
Hecne , the required ratio is $1 : \sqrt{3}$

|

Updated on:21/07/2023

Class 10 MATHS SURFACE AREAS AND VOLUMES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A solid is hemispherical at the bottom and conical (of same radius) above it . If the surface areas of the two parts are equal then the ratio of its radius and the slant height of the conical part is
A $1 : 2$
B $2 : 1$
C $1 : 4$
D $4 : 1$
Question 2 - Select One
A solid hemisphere is or radius 11 cm. The curved surface area in sq. cm is
A1140.85
B $1386.00$
C760.57
D860.57
Question 3 - Select One
A sphere and a hemisphere have the same volume. The ratio of their curved surface area is :
A $2^{- \frac{3}{2}} : 1$
B $2^{\frac{2}{3}} : 1$
C $4^{- \frac{2}{3}} : 1$
D $2^{\frac{1}{3}} : 1$

RS AGGARWAL-VOLUME AND SURFACE AREAS OF SOLIDS-MULTIPLE-CHOICE QUESTIONS(MCQ)

Home
Ask Doubt
Profile