Theorem 7.4 (SSS congruence rule) : If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
let PQR and XYZ be two traingles,
Steps:---
draw xw intersecting yz such that
∠WYZ=∠PQR and
WY=PQ
Proof:---
In △PQR and △WYZ
PQ=WY
∠PQR=∠WYZ
QR=YZ
△PQR==△WYZ(SAS rule)
Thus,∠W=∠P.........(1)
In △XYW
PQ=WY=XY
So,WY=XY
∠1=∠2.....(2)
Similary,
∠3=∠4....(3)
adding (2) and(3)
∠1+∠3=∠2+∠4
⇒∠x=∠W=∠P[from(1)]
Now,in △PQR and △XYZ
PQ=XY
∠P=∠X
PR=XZ
Thus,△PQR==△XYZ
Hence,showed.
Topper's Solved these Questions
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 7.5
Explore 1 Video
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 7.6
Explore 1 Video
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 7.3
Explore 1 Video
- LINES AND ANGLESBook:NCERTChapter:LINES AND ANGLESExercise:SOLVED EXAMPLES
Explore 8 Videos
- NUMBER SYSTEMSBook:NCERTChapter:NUMBER SYSTEMSExercise:EXERCISE 1.4
Explore 2 Videos
Similar Questions
Assertion (A) : If two triangle have same perimeter , then they are congruent.
Reason (R) : If under a given correspondence, the three sides of one triangle are equal to the three sides of the other triangle, then the two triangles are congruent.
View SolutionIf any two angles and a non-included side of one triangle are equal to the corresponding angles and side of another triangle, then the two triangles are congruent. GIVEN : Two sABC and DEF such that ∠A=∠D,∠B=∠E,BC=EF TO TROVE : ABC≅DEF
View Solution
Knowledge Check
Consider the following statements :
(1) If three sides of a triangle are equal to three sides of another triangle, then the triangles are congruent.
(2) If three angles of a triangles are equal to three angles of another triangle respectively, then the two triangles are congruent. Of these statements :A1 is correct and 2 is falseBboth 1 and 2 are falseCboth 1 and 2 are correctD1 is false and 2 is correctConsider the following statements :
(1) If three sides of a triangle are equal to three sides of another triangle, then the triangles are congruent.
(2) If three angles of a triangles are equal to three angles of another triangle respectively, then the two triangles are congruent. Of these statements :A1 is correct and 2 is falseBboth 1 and 2 are falseCboth 1 and 2 are correctD1 is false and 2 is correctIf in two right triangles, the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent. 1.
PL is an altitude from P of ΔPQR on QR such that QL = LR. Then,A∠Q<∠RB∠Q=∠RC∠Q>∠RD∠P=∠R
Which of the following statements are true and which of them are false?
(i) All squares are congruent.
(ii) If two squares have equal areas, they are congruent.
(iii) If two figures have equal areas, they are congruent.
(iv) If two triangles are equal in area, they are congruent.
(v) If two sides and one angle of a triangle are equal to the corresponding two sides and angle of another triangle, the triangles are congruent.
(vi) If two angles and any side of a triangle are equal to the corresponding angles and the side of another triangle then the triangles are congruent.
(vii) If three angles of a triangle are equal to the corresponding angles of another triangle then the triangles are congruent.
(viii) If the hypotenuse and an acute angle of a right triangle are equal to the hypotenuse and the corresponding acute angle of another right triangle then the triangles are congruent.
(ix) If the hypotenuse of a right triangle is equal to the hypotenuse of another right triangle then the triangles are congruent.
View SolutionAngle Angle Side (AAS) Congruence - If any two angles and a non-included side of one triangle are equal to the corresponding angles and side of another triangle; the two ttriangles are congruent.
View SolutionTwo triangles are congruent if three angles of one triangle are equal to three angles of the other triangle.
View SolutionWhich of the following statements are true (T) and which are false (F): Side opposite to equal angles of a triangle may be unequal. Angle opposite to equal sides of a triangle are equal. The measure of each angle of an equilateral triangle is 600. If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles. The bisectors of two equal angles of a triangle are equal. If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles. The two altitudes corresponding to two equal sides of a triangle need not be equal. If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent. Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
View SolutionIf in two right triangles, the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent. 1.
In the figure, it is given that LM=MN,QM=MR,ML⊥PQandMN⊥PR. then
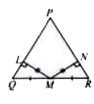
View Solution

