Two equal positive charges are kept at points A and B. The electric potential at the points between A and B (exculding these points ) is studid while moving from A to b. The potential
To solve the problem of electric potential between two equal positive charges located at points A and B, we can follow these steps:
1. Understanding the Setup:
- We have two equal positive charges, Q, located at points A and B, separated by a distance R.
- We want to analyze the electric potential at points between A and B, excluding A and B themselves.
2. Electric Potential Formula:
- The electric potential V due to a point charge is given by the formula:
V=kQr
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge to the point where the potential is being measured.
3. Calculating Potential at a Point Between A and B:
- Let’s denote a point between A and B as point P, which is at a distance x from point A. Therefore, the distance from point B to point P will be R−x.
- The total electric potential VP at point P due to both charges is:
VP=VA+VB=kQx+kQR−x
4. Analyzing the Behavior of Potential:
- As we move from point A to point B (i.e., as x increases from 0 to R):
- When x is very small (close to A), kQx becomes very large, and kQR−x is relatively small.
- As x approaches R (close to B), kQx becomes smaller, and kQR−x becomes very large.
- Therefore, the potential starts high near A, decreases to a minimum at some point, and then increases again as we approach B.
5. Finding the Minimum Potential:
- To find the exact point where the potential is minimum, we can differentiate VP with respect to x and set the derivative equal to zero:
dVPdx=−kQx2+kQ(R−x)2=0
- This leads to:
1x2=1(R−x)2
- Solving this gives x=R2, indicating that the minimum potential occurs at the midpoint between A and B.
6. Conclusion:
- The electric potential decreases from a maximum at point A, reaches a minimum at the midpoint between A and B, and then increases again towards point B.
Final Answer:
The potential at points between A and B decreases initially, reaches a minimum at the midpoint, and then increases again as we approach point B.
---
- We have two equal positive charges, Q, located at points A and B, separated by a distance R.
- We want to analyze the electric potential at points between A and B, excluding A and B themselves.
- The electric potential V due to a point charge is given by the formula:
V=kQr
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge to the point where the potential is being measured.
- Let’s denote a point between A and B as point P, which is at a distance x from point A. Therefore, the distance from point B to point P will be R−x.
- The total electric potential VP at point P due to both charges is:
VP=VA+VB=kQx+kQR−x
- As we move from point A to point B (i.e., as x increases from 0 to R):
- When x is very small (close to A), kQx becomes very large, and kQR−x is relatively small.
- As x approaches R (close to B), kQx becomes smaller, and kQR−x becomes very large.
- Therefore, the potential starts high near A, decreases to a minimum at some point, and then increases again as we approach B.
- To find the exact point where the potential is minimum, we can differentiate VP with respect to x and set the derivative equal to zero:
dVPdx=−kQx2+kQ(R−x)2=0
- This leads to:
1x2=1(R−x)2
- Solving this gives x=R2, indicating that the minimum potential occurs at the midpoint between A and B.
- The electric potential decreases from a maximum at point A, reaches a minimum at the midpoint between A and B, and then increases again towards point B.
The potential at points between A and B decreases initially, reaches a minimum at the midpoint, and then increases again as we approach point B.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBook:HC VERMAChapter:ELECTRIC FIELD AND POTENTIALExercise:Objective 2
Explore 8 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMAChapter:ELECTRIC FIELD AND POTENTIALExercise:Exercises
Explore 75 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMAChapter:ELECTRIC FIELD AND POTENTIALExercise:Short Answer
Explore 14 Videos
- ELECTRIC CURRENT THROUGH GASESBook:HC VERMAChapter:ELECTRIC CURRENT THROUGH GASESExercise:Exercises
Explore 23 Videos
- ELECTROMAGNETIC INDUCTIONBook:HC VERMAChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE
Explore 9 Videos
Similar Questions
Knowledge Check
Two equal positive charges are kept at points A and B. The electric potential at the points between A and B (exculding these points ) is studid while moving from A to b. The potential
AContinuously increasesBContinuously decreasesCIncreases and decreasesDDecreases then increasesThe figure shows a arrangement of capacitors and a battery.

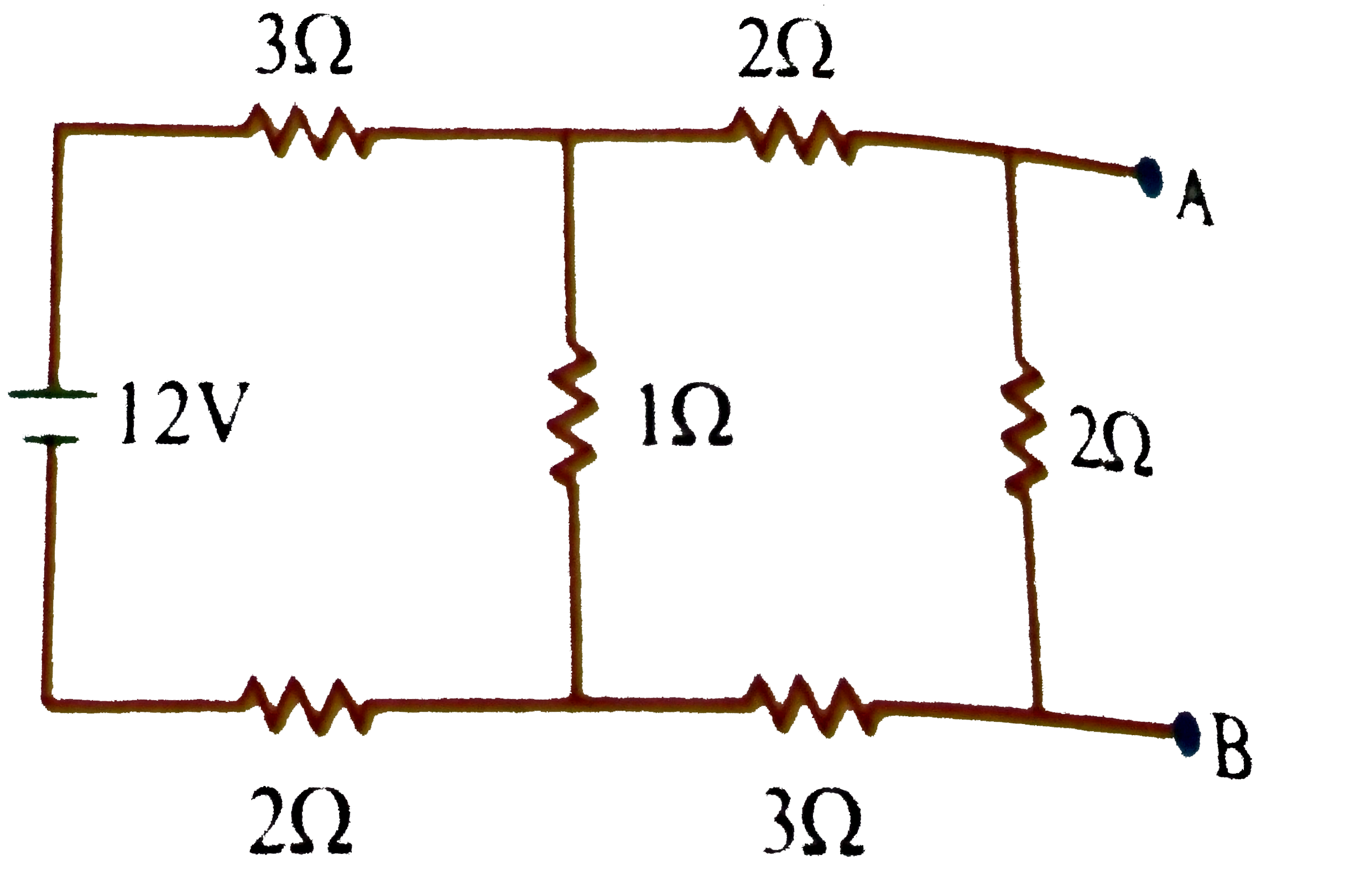
The potential of the points B and D are (if VC=0)AVE=8VBVE=12VCVD=8VDVD=12VThe potential difference between point A and B is
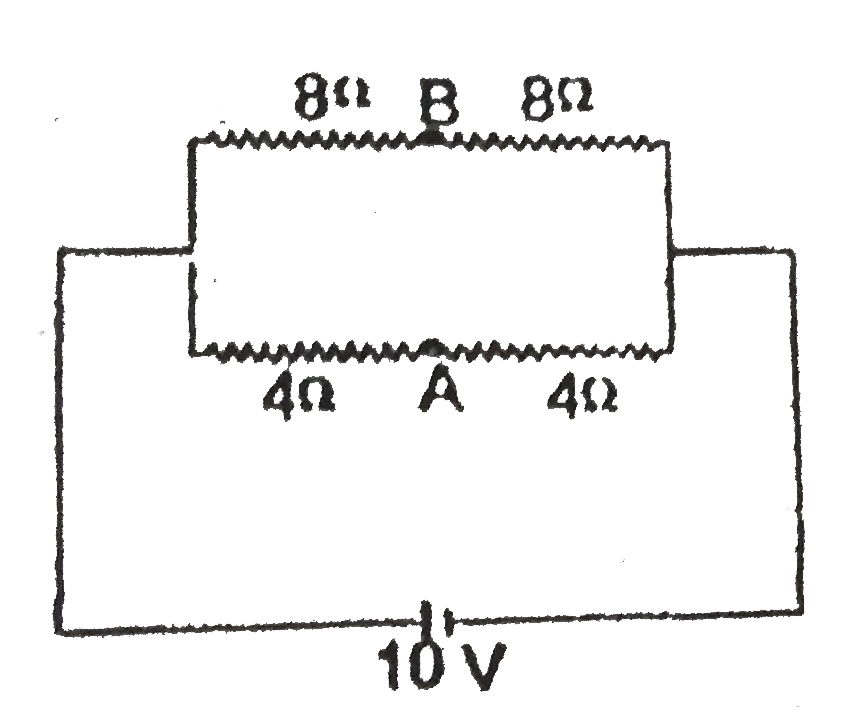 A207VB407VC107VDzero
A207VB407VC107VDzero
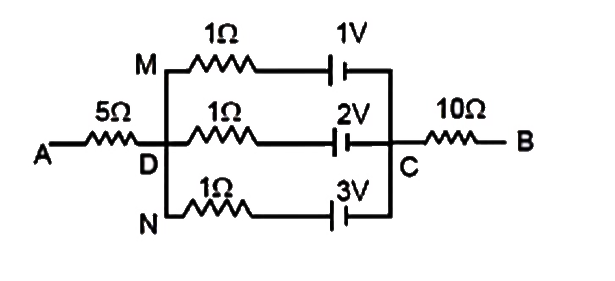
The potential difference between points A and B is -
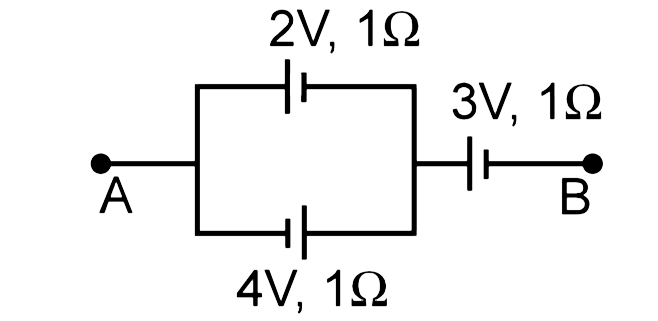
View SolutionThe potential difference between points A and B is
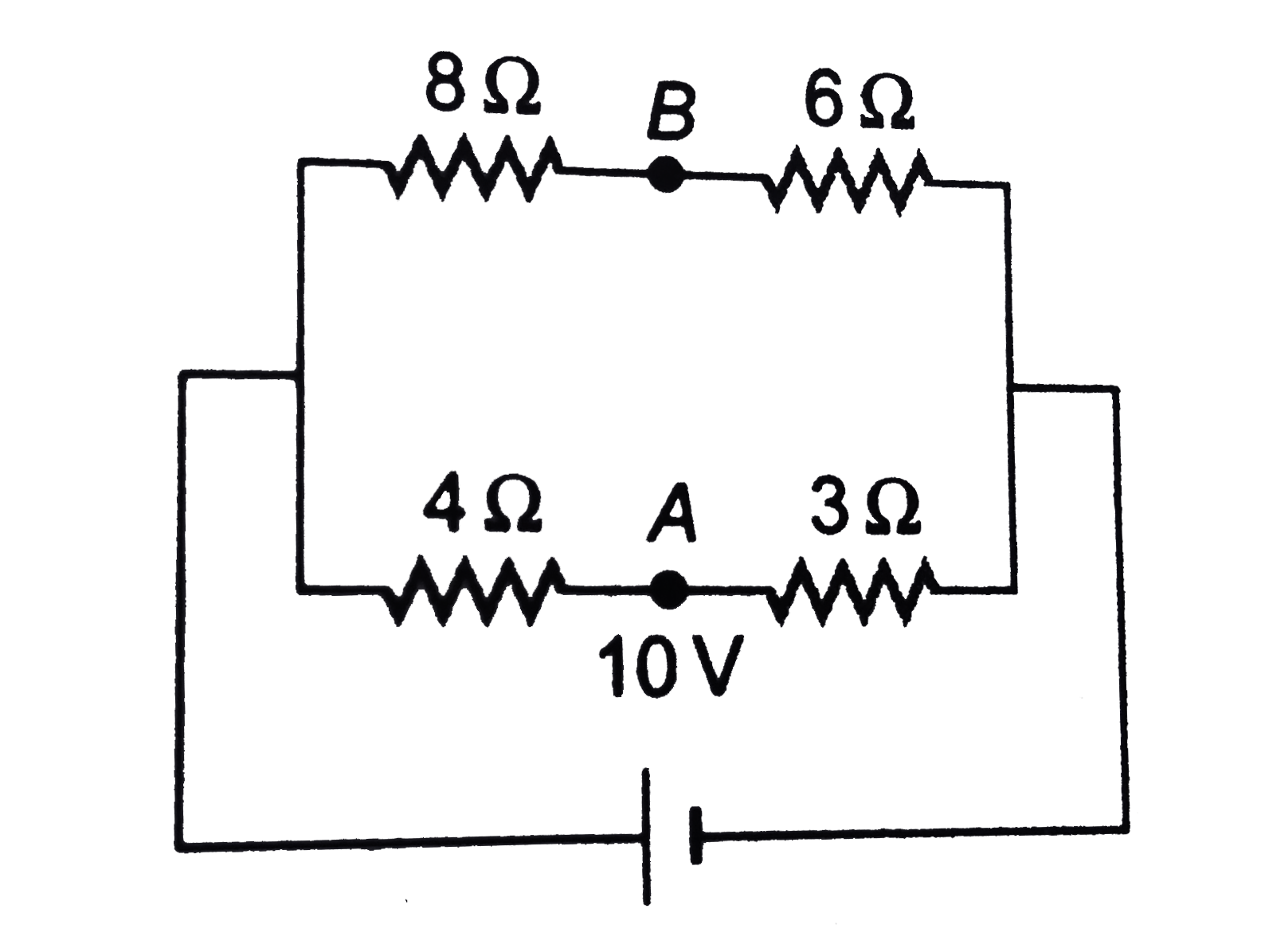
View SolutionThe potential difference between points A and B is:
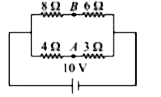
View SolutionThe potential difference between points A nd B is
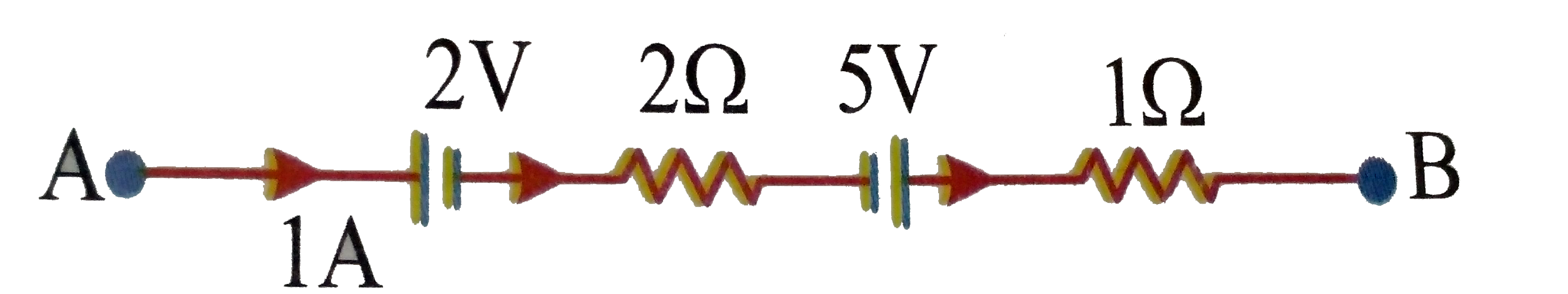
View SolutionA, B and C are three points in a uniform electric field. The electric potential is
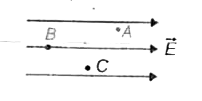
View Solution