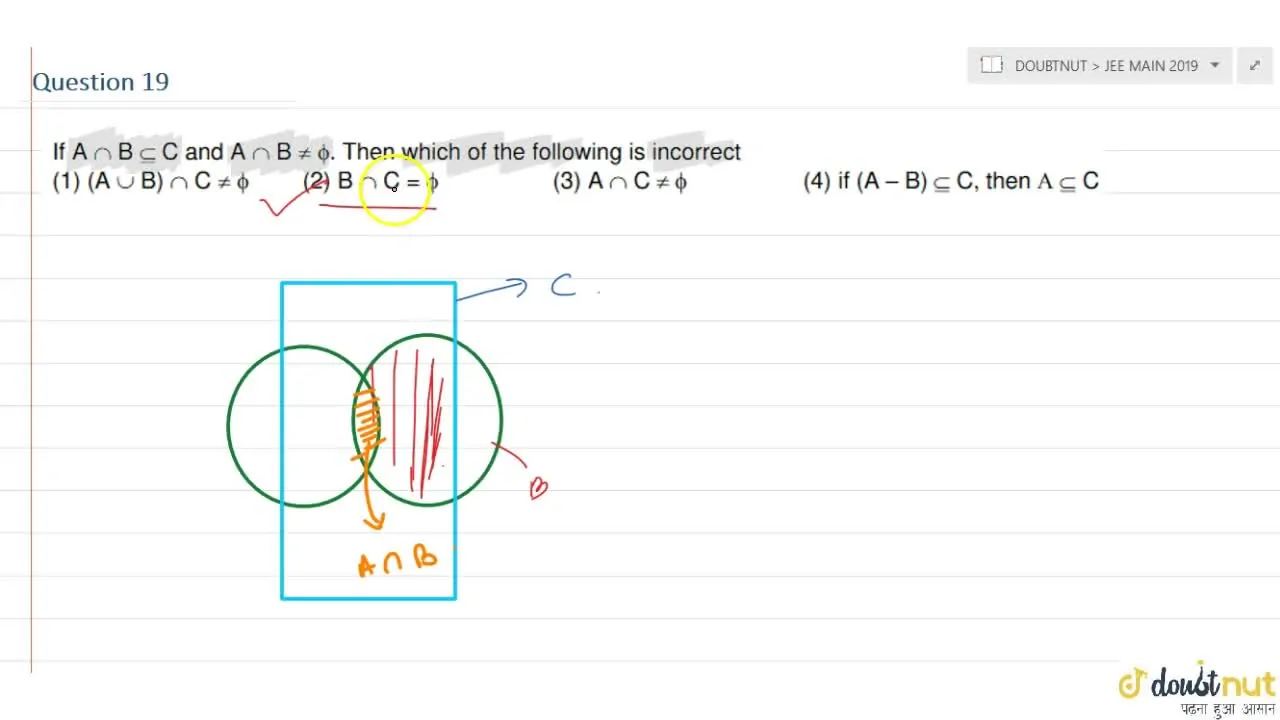
Let A,B and C be sets such that A∩B⊆C and A∩B≠ϕ. Then which of the following statements is not true?
B∩C≠ϕ
If (A−B)⊆C, then A⊆C
C(∪A)∩(C∪B)=C
If (A−C)⊆B, then A⊆B
The correct Answer is:A
Step by step video, text & image solution for Let A,B and C be sets such that Ann B sube C and Ann B != phi. Then which of the following statements is not true? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
Let A,B and C be sets such that A∩B⊆C and A∩B≠ϕ. Then which of the following statements is not true?
View SolutionIa A∩B⊆C and AcapBcancel=phi. Then which of the following is incorrect
View SolutionIf B⊆A, which of the following statements is correct ?
View SolutionLet A and B be two non-null events such that A⊆B. Then, which of the following statements is always correct?
View SolutionLet A, B and C be the sets such that A∪B=A∪C and A∩B=A∩C. show that B=C
View SolutionLet A,B and C be the sets such that A∪B=A∪C and A∩B=A∩C .Show that B=C
View SolutionWhich of the following is ann oxidizing agent?
View SolutionWhich of the following is ann oxidizing agent?
View SolutionLet a,b and c be three unit vectors such that 3a+4b+5c=0. Then which of the following statements is true?
View SolutionIf A and B are two sets such that A×B=ϕ, then which of the following must be true ?
View Solution