Find the derivative of the function f(x)=2x2+3x−5at x=−1. Also prove that f′(0)+3f′(−1)=0.
Given function is:
f(x)=2x2+3x−5
Differentiating with respect to x we get:
f'(x)=4x+3
So, f'(−1)=4(−1)+3=−1
f'(0)=4(0)+3=3
f'(0)+3f'(−1)=3−3=0
Topper's Solved these Questions
- LIMITS AND DERIVATIVESBook:NCERTChapter:LIMITS AND DERIVATIVESExercise:MISCELLANEOUS EXERCISE
Explore 30 Videos
- LIMITS AND DERIVATIVESBook:NCERTChapter:LIMITS AND DERIVATIVESExercise:EXERCISE 13.2
Explore 11 Videos
- LIMITS AND DERIVATIVESBook:NCERTChapter:LIMITS AND DERIVATIVESExercise:EXERCISE 13.3
Explore 8 Videos
- INTRODUCTION TO THREE DIMENSIONAL GEOMETRYBook:NCERTChapter:INTRODUCTION TO THREE DIMENSIONAL GEOMETRYExercise:EXERCISE 12.1
Explore 4 Videos
- LINEAR INEQUALITIESBook:NCERTChapter:LINEAR INEQUALITIESExercise:EXERCISE 6.2
Explore 10 Videos
Similar Questions
Find the derivative of the function f(x)=2x2+3x−5at x=−1. Also prove that f′(0)+3f′(−1)=0.
View SolutionFind the derivative of f(x)=2x2+3x−5 at x=−1. Also, prove that f'(0)+3f'(−1)=0.
View SolutionFind the derivatives of the following (1-3) functions :
f(x)=x3+4x2+3x+2
View SolutionDraw the graph of the function
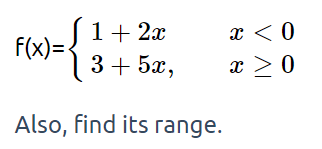
View SolutionFind the range of the function f(x)=cot−1(log)0.5(x4−2x2+3)
View SolutionFind fof−1 and f−1 of for the function :
f(x)=1x,x≠0. Also prove that fof−1=f−1of.
View SolutionLet f(x+y)=f(x)f(y) for all x and y . Suppose f(5)=2 and f′(0)=3 , find f′(5) .
View SolutionA function y=f(x) satisfies the differential equation dydx+x2y=−2x,f(1)=1. The value of ∣∣f''(1)∣∣ is
View SolutionShow that the function f(x)={x2sin(1x),ifx≠00,ifx=0 is differentiable at x=0 and f′(0)=0
View SolutionFind the one-sided limits of the functions :
f(x)={−2x+3ifx≤13x−5ifx>1asx→1:
(b) f(x)=x2−1|x−1|asx→1
(c ) f(x)=√1−cos2xx as x→0
(d) f(x)=3+11+71/(1−x)asx→1
(e) f(x)=cos(π2)asx→0
(f) f(x)=5/(x−2)3asx→2
View Solution
