Derive an expression for the kinetic energy of a body rotating with constant angular velocity. State how it depends on the moment of inertia, and frequency and period of rotation.
Video Solution
Text Solution
Consider a rigid body rotating with a constant angular velocity →ω about an axis through the point O and perpendicular to the plane of the figure. Suppose that the body consists of N particles of masses m1,m2,…,mN situated at distances r1,r2,...,rN respectively from tha axis of rotation as shown in the figure.
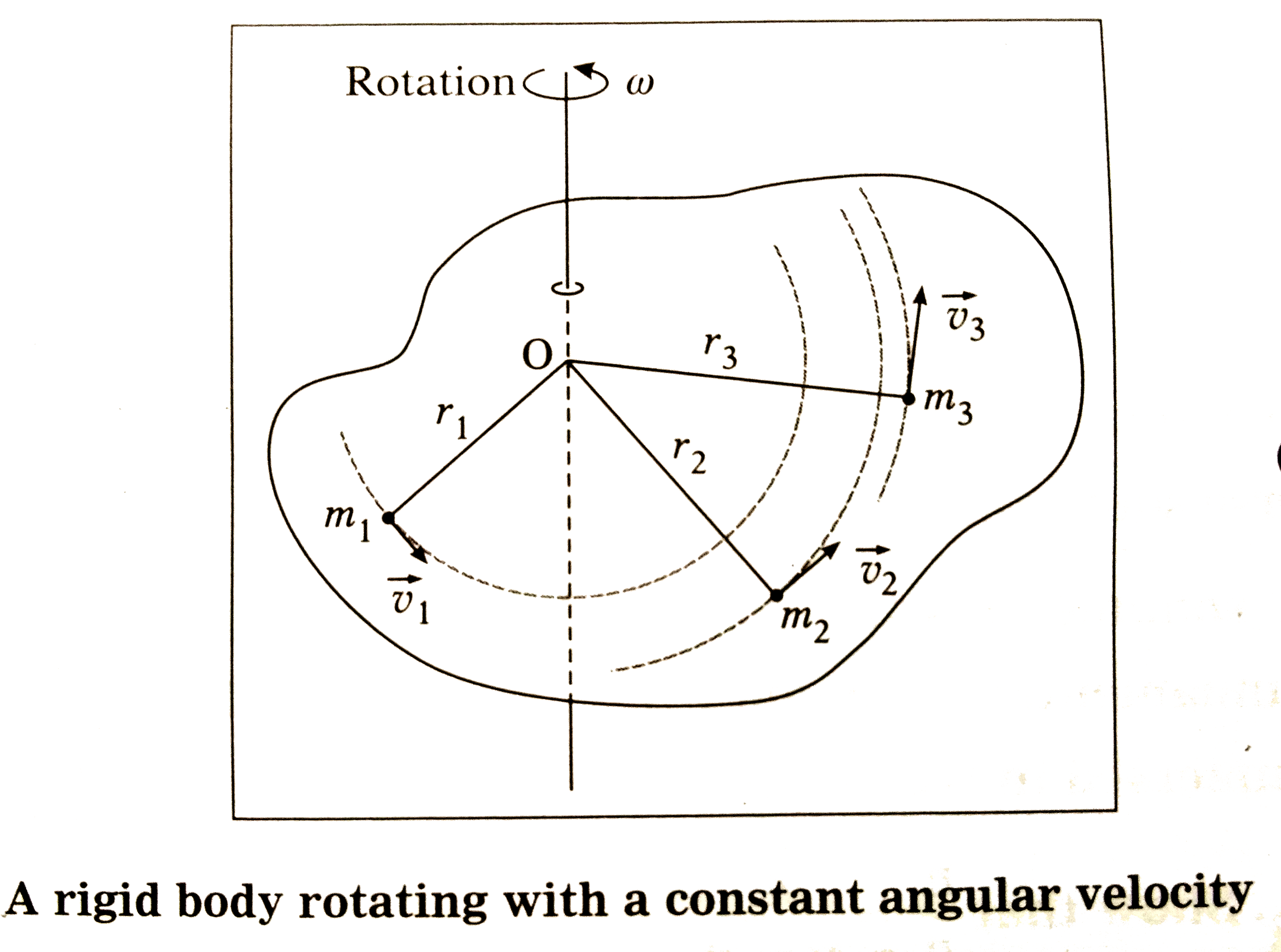
A rigid body rotating with a constant angular velocity
As the body rotates , all the particles perform uniform circular motion with the same angular velocity →ω . However , various particles of the body have different linear speeds depending upon their distances from the axis of rotation .
The linear speed of the particle with mass m1 is v1=r1ω. Therefore, its kinetic energy is
E1=12m1v21=12m1r21ω2 ...(1)
Similarly , the kinetic energy of the particle with mass m2 is
E2=12m2v22=12m2r22ω2,and so on .
The rotational kinetic energy (E) of the body is
E=E1+E2+...+EN
=12m1r21ω2+12m2r22ω2+...+12mNr2Nω2
=12[m1r21+m2r22+...+mNr2N]ω2=12(N∑i=1mir2i)ω2
∴E=12Iω2 ....(2)
where I=N∑i=1mir2i is the moment of inertia of the body about the axis of rotation.
If f is the frequency of rotation of the body and T the period of rotation, then ω=2πf=2πT
∴E=12I(2πf)2=2π2If2=2π2IT2 ....(3)
Thus, from Eqs. (2) and (3) , the rotational kinetic energy of a body is proportional to (1) its moment of inertia about the given rotation axis (2) the square of its angular speed ( or frequency of rotation ) or inverse square of its rotational period .
|
Topper's Solved these Questions
- MODEL QUESTION PAPER Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:MODEL QUESTION PAPER Exercise:SECTION- C
Explore 12 Videos
- LAWS AND THEORIESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:LAWS AND THEORIESExercise:Assignments
Explore 2 Videos
- MODEL QUESTION PAPER FOR PRACTICEBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:MODEL QUESTION PAPER FOR PRACTICEExercise:SECTION-D
Explore 5 Videos
Similar Questions
Knowledge Check
The kinetic energy of a rotating body depends upon
Adistribution of mass onlyBangular speed onlyCdistribution of mass and angular speedDangular acceleration onlyThe kinetic energy of a rotating body depends upon
Adistribution of mass onlyBongular speed onlyCdestribution of mass and angular speedDangular acceleration onlyFor a body rotating with constant angular velcoity, its kinetic energy is directly proportional to the square of its
Afrequency of rotationBrotational periodCradius of gyrationDboth (a) and (c )
Obtain an expression for the kinetic energy of a particle performing linear SHM. State how it depends upon the amplitude, frequency and period of SHM.
View SolutionObtain an expression for torque acting on a rotating body with constant angular acceleration. Hence state the dimensions and SI unit of torque.
View SolutionThe moment of inertia of a body depends upon
View SolutionOn what factors does the kinetic energy of a purely rotating body depend?
View SolutionIf the angular velocity of a rotating rigid body is increased then its moment of inertia about that axis
View Solution

