prove that the charge induced does not depend on the rate of change of magnetic flux.
Consider a rectangular wire loop PQRS of width l, with its plane perpendicular to a uniform magnetic field of induction →B. The loop is being pulled out of the magnetic field at a constant speed v, as shown.
At any instant, let x be the length of the part of the loop in the magnetic field. Then, the magnetic flux through the loop is
Φ=Blx ...(1)
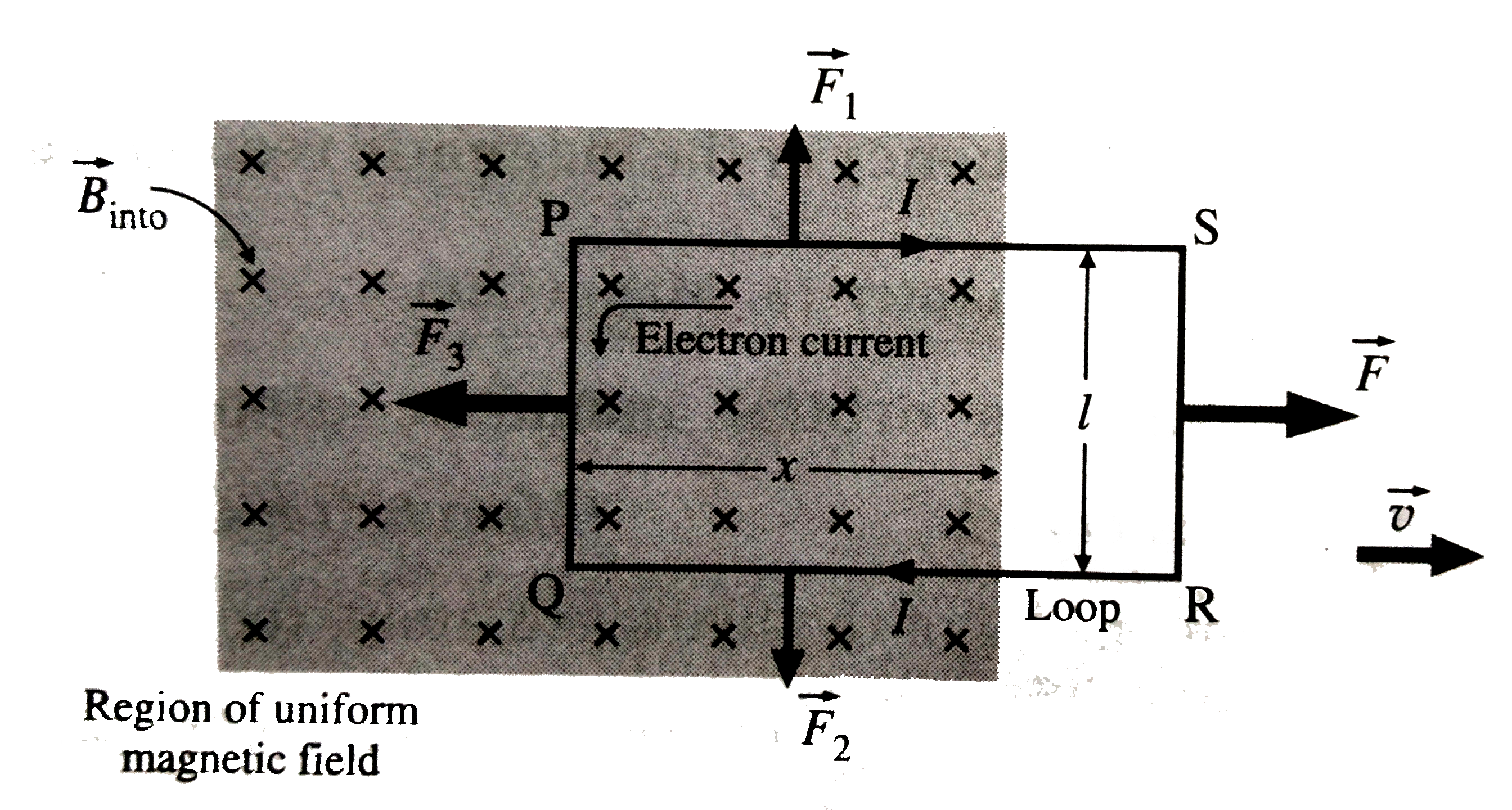
As the loop moves to the right through a distance dx = vdt in time dt, the area of the loop inside the field changes by dA=ldx=lvdt.
And, the change in the magnetic flux dΦ through the loop is
dΦ=Bda=Blvdt ...(2)
Then, the time rate of change of magnetic flux is
dΦdt=Blvdtdt=Blv ...(3)
The changing magnetic flux induces a current I in the clockwise direction, as shown. a current-carrying conductor in a magnetic field experiences a force →F=I→L×→B (in the usual notation), whose direction can be found using Fleming's left hand rule. Accordingly, forces →F1and→F2 on wires PS and QR, respectively, are equal in magnitude (=IxB), opposite in direction and have the same line of action. Hence, they balance each other. There is no force on wire RS as it lies outside the field.
The force →F3 on wire PQ has magnitude F3=IlB and is directed towards the left.
To move the loop with constant velocity →v, an external force →F=−→F3 must be applied.
The work done by the external agent is
dW=Fdx=−IlBdx=−IBdA=−IdΦ [from Eq. (2)] ...(4)
Therefore, the power, i.e., the time rate of doing work, is
P=dWdt=I(−dΦdt) ...(5)
The electric power when an emf E drives a current through a circuit is given by
P=EI ...(6)
In Eq. (4), P is the electric power when a current I is driven through a circuit as a consequence of a change in the magnetic flux through it.
From Eqs. (5) and (6), dW=Pdt=EIdt ...(7)
Therefore, comparing Eq. (4) with Eq. (7), E=−dΦdt ...(8)
Thus, the emf induced in an electric circuit is equal to the negative of the time rate of change of the magnetic flux through the circuit, which is Faraday-Lenz's law.
Topper's Solved these Questions
- DERIVATIONS-IIBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:DERIVATIONS-IIExercise:Atoms, Molecules and Nuclei
Explore 7 Videos
- DERIVATIONS-IIBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:DERIVATIONS-IIExercise:Semiconductors
Explore 1 Video
- DERIVATIONS-IIBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:DERIVATIONS-IIExercise:Magnetism
Explore 1 Video
- DERIVATIONS-IBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:DERIVATIONS-IExercise:Assignments
Explore 9 Videos
- DISTINGUISH BETWEENBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:DISTINGUISH BETWEENExercise:Assingment
Explore 3 Videos
Similar Questions
Knowledge Check
Assertion (A): Whenever the magnetic flux linked with a closed coil changes there will be an induced emf as well as an induced current.
Reason (R ) : Accroding to Faraday, the induced emf is inversely proportional to the rate of change of magnetic flux linked with a coil.ABoth A and R are true and R is the correct explanation of ABBoth A and R are true and R is not the correct explanation of ACA is true but R is falseDA is false but R is true.STATEMENT-1: Lenz's law is based on the principle of conservation of energy. Because
STATEMENT-2: The magnitude of the induced emf is directly proportional to the rate of change of the magnetic flux.AStatement-1 is True , Statement-2 is True , Statement-2 is a correct explanation for Statement-1.BStatement-1 is True , Statement-2 is True , Statement-2 is NOT a correct explanation for Statement-1.CStatement-1 is True , Statement-2 is FalseDStatement-1 is False , Statement-2 is TrueThe resistance of a coil is 5 ohm and a current of 0.2A is induced in it due to a varying magnetic field. The rate of change of magnetic flux in it will be-
A0.5 W/bB0.05 Wb/sC1 W b/sD20 Wb/s
Statement-1 : The induced e.m.f. and current will be same in two identical loops of copper and aluminium, when rotated with same speed in the same magnetic field.
Statement-2 : Induced e.m.f. is proportional to rate of change of magnetic field while induced current depends on resistance of wire.
View SolutionThe magnitude of the induced current in a closed circuit is equal to the time rate of change of magnetic flux through the circuit.
View SolutionThe electric displacement current through a surface area "S" is proportional to the Magnetic flux through S. Rate of change of magnetic flux through S Electric flux through S, Rate of change of electric flux through S
View SolutionThe induced e.m.f. in a coil does not depend on
View SolutionAssertion: Magnetic field B (shown inwards) varies with time t as shown. At time to induced current in the loop is clockwise
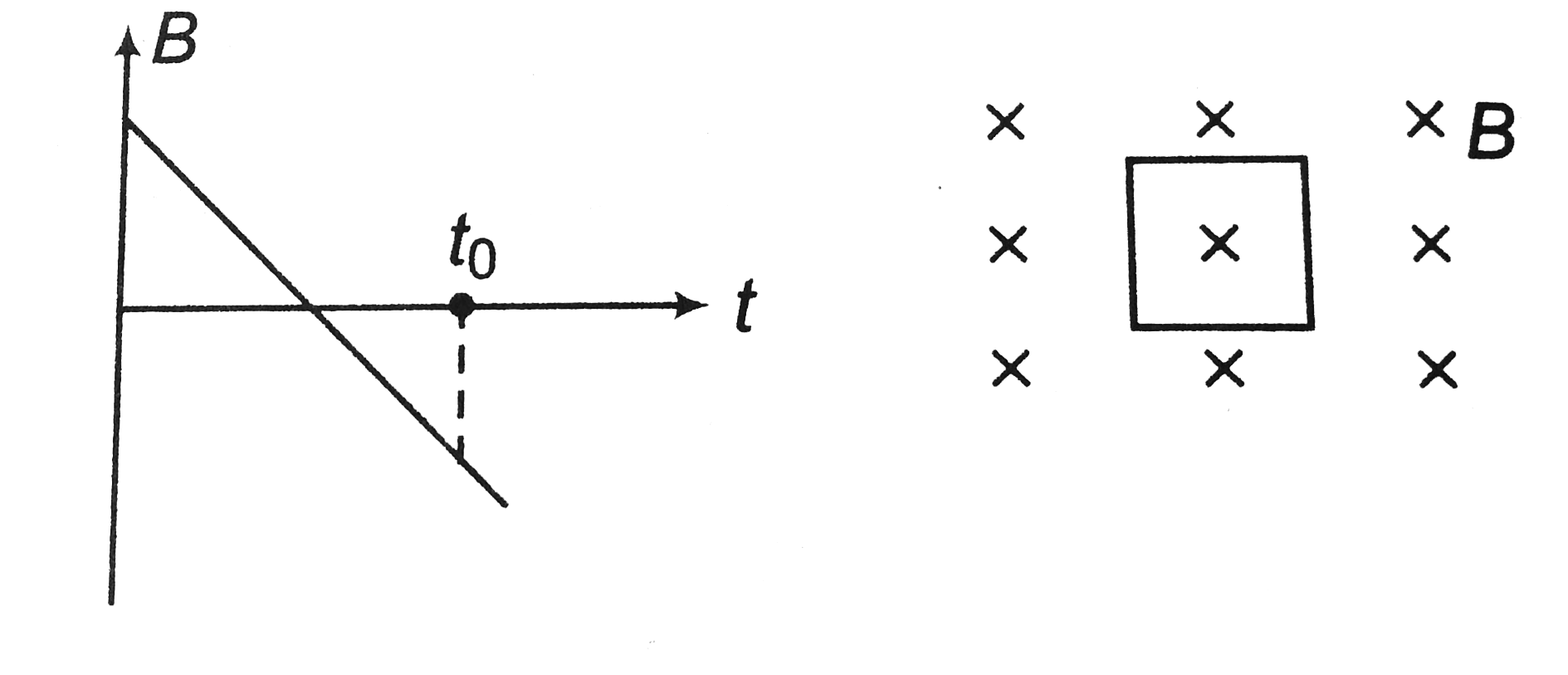
Reason : If rate of change of magnetic flux from a coil is constant, charge should flow in the coil at a constant rate.
View Solution

