WAVEFRONT
A wavefront is defined as a surface of all neighbouring points which receive light waves from a source at the same instant and are in the same phase .
Topper's Solved these Questions
- DEFINITIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DEFINITIONSEXERCISE - INTERFERENCE AND DIFFRACTION
5 Videos
- DEFINITIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DEFINITIONSEXERCISE - ELECTROSTATICS
9 Videos
- DEFINITIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DEFINITIONSEXERCISE - KINETIC THEORY OF GASES AND RADIATION
10 Videos
- DERIVATIONS-IBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DERIVATIONS-IEXERCISE - Assignments
9 Videos
Similar Questions
In the given figure, a wavefront AB moving in air is incident on a plane glass surface XY, Its position CD after refraction through a glass slab is showin in gigure. The ratio of width of wavefront AB to the refracted wavefront CD is
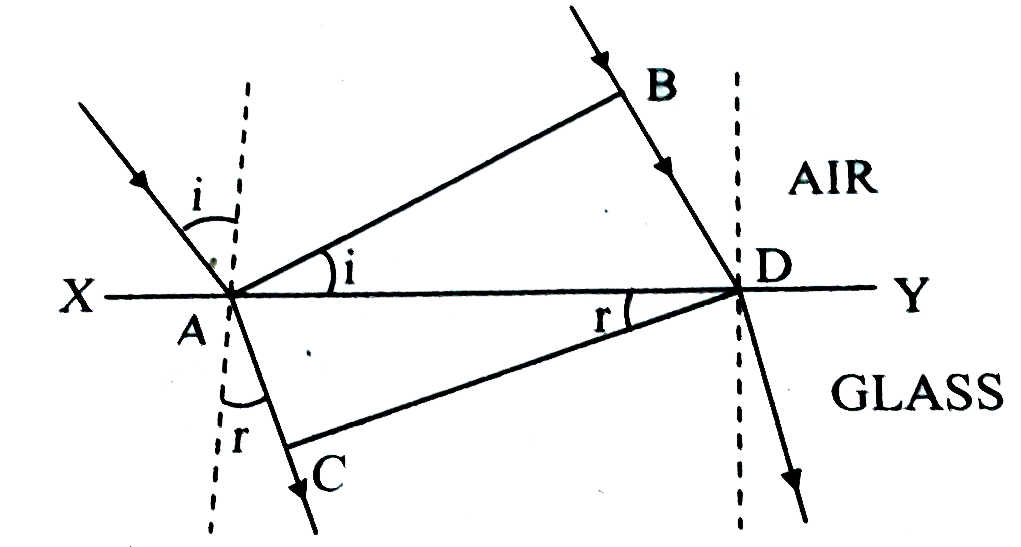
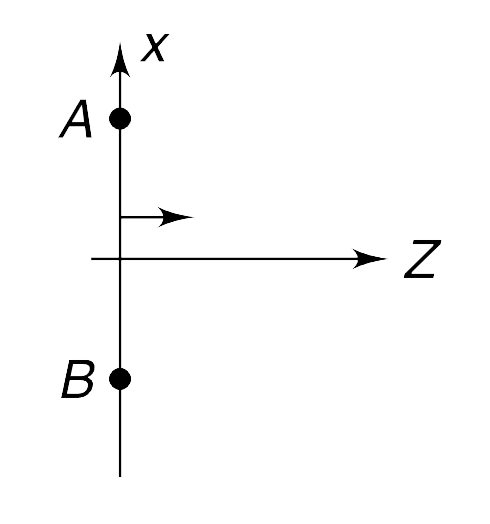
View SolutionThe refractive index of a medium changes asμ=μ0[1−x2+y2d2]1/2where μ0 is the refractive index on the z axis. A plane wavefront (AB) is incident along z axis as shown in the figure. Draw the wavefront at a later timeΔt. Is the wavefront getting focused?
View Solution
Knowledge Check
Choose the correct option:
(i) A surface on which the wave disturbance in same phase at all points is called a wavefront.
(ii) The direction of a wave at a point is perpendicular to the wavefront through that point.
(iii) The wavefronts of a wave originating from a point source is spherical.
The wavefronts for a wave going along a fixed direction are planes perpendicular to that direction.A(i), (ii)B(ii), (iii), (iv)C(i), (ii), (iii)Dall_E01_075_Q01.png)
Huygen was the figure scientist who proposed the idea of wave theory of light he said that the light propagates in form of wavelengths. A wavefront is a imaginary surface of every point of which waves are in the same. phase.
For example the wavefront for a point source of light is collection of concentric spheres which have centre at the origin w1 is a wavefront w2 is another wavefront.
The radius of the wavefront at time 't' is 'ct' in thic case where 'c' is the speed of light the direction of propagation of light is perpendicular to the surface of the wavelength. the wavefronts are plane wavefronts in case of a parallel beam of light.
_E01_075_Q02.png)
Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be considered only in the forward direction (i.e., the direction of propagation of light) and not in the reverse direction if a wavefront w1 and draw spheres of radius 'cΔt' they are called secondary wavelets.
Draw a surface w2 which is tangential to all these secondary wavelets w2 is the wavefront at time t+Δt Huygen proved the laws of reflection and laws of refraction using concept of wavefront.
Q._E01_075_Q03.png)
Spherical wavefronts shown in figure, strike a plane mirror. reflected wavefront will be as shown inA_E01_075_O01.png) B
B_E01_075_O02.png) C
C_E01_075_O03.png) D
D_E01_075_O04.png)
_E01_076_Q01.png)
Huygen was the figure scientist who proposed the idea of wave theory of light he said that the light propagates in form of wavelengths. A wavefront is a imaginary surface of every point of which waves are in the same. phase.
For example the wavefront for a point source of light is collection of concentric spheres which have centre at the origin w1 is a wavefront w2 is another wavefront.
The radius of the wavefront at time 't' is 'ct' in thic case where 'c' is the speed of light the direction of propagation of light is perpendicular to the surface of the wavelength. the wavefronts are plane wavefronts in case of a parallel beam of light.
_E01_076_Q02.png)
Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be considered only in the forward direction (i.e., the direction of propagation of light) and not in the reverse direction if a wavefront w1 and draw spheres of radius 'cΔt' they are called secondary wavelets.
Draw a surface w2 which is tangential to all these secondary wavelets w2 is the wavefront at time t+Δt Huygen proved the laws of reflection and laws of refraction using concept of wavefront.
Q._E01_076_Q03.png)
Wavefronts incident on an interface between the media are shown in the figure. the refracted wavefront will be as shown inA_E01_076_O01.png) B
B_E01_076_O02.png) C
C_E01_076_O03.png) D
D_E01_076_O04.png)
_E01_074_Q01.png)
Huygen was the figure scientist who proposed the idea of wave theory of light he said that the light propagates in form of wavelengths. A wavefront is a imaginary surface of every point of which waves are in the same. phase.
For example the wavefront for a point source of light is collection of concentric spheres which have centre at the origin w1 is a wavefront w2 is another wavefront.
The radius of the wavefront at time 't' is 'ct' in thic case where 'c' is the speed of light the direction of propagation of light is perpendicular to the surface of the wavelength. the wavefronts are plane wavefronts in case of a parallel beam of light.
_E01_074_Q02.png)
Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be considered only in the forward direction (i.e., the direction of propagation of light) and not in the reverse direction if a wavefront w1 and draw spheres of radius 'cΔt' they are called secondary wavelets.
Draw a surface w2 which is tangential to all these secondary wavelets w2 is the wavefront at time t+Δt Huygen proved the laws of reflection and laws of refraction using concept of wavefront.
Q. A point source of light is placed at origin, in air. the equation of wavefront of the wave at time t, emitted by source at t=0 is (take refractive index of air as 1)
View Solution_E01_077_Q01.png)
Huygen was the figure scientist who proposed the idea of wave theory of light he said that the light propagates in form of wavelengths. A wavefront is a imaginary surface of every point of which waves are in the same. phase.
For example the wavefront for a point source of light is collection of concentric spheres which have centre at the origin w1 is a wavefront w2 is another wavefront.
The radius of the wavefront at time 't' is 'ct' in thic case where 'c' is the speed of light the direction of propagation of light is perpendicular to the surface of the wavelength. the wavefronts are plane wavefronts in case of a parallel beam of light.
_E01_077_Q02.png)
Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be considered only in the forward direction (i.e., the direction of propagation of light) and not in the reverse direction if a wavefront w1 and draw spheres of radius 'cΔt' they are called secondary wavelets.
Draw a surface w2 which is tangential to all these secondary wavelets w2 is the wavefront at time t+Δt Huygen proved the laws of reflection and laws of refraction using concept of wavefront.
Q._E01_077_Q03.png)
Plane are incident on a spherical mirror as shown in the figure. the reflected wavefronts will be
View Solution_E01_078_Q01.png)
Huygen was the figure scientist who proposed the idea of wave theory of light he said that the light propagates in form of wavelengths. A wavefront is a imaginary surface of every point of which waves are in the same. phase.
For example the wavefront for a point source of light is collection of concentric spheres which have centre at the origin w1 is a wavefront w2 is another wavefront.
The radius of the wavefront at time 't' is 'ct' in thic case where 'c' is the speed of light the direction of propagation of light is perpendicular to the surface of the wavelength. the wavefronts are plane wavefronts in case of a parallel beam of light.
_E01_078_Q02.png)
Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be considered only in the forward direction (i.e., the direction of propagation of light) and not in the reverse direction if a wavefront w1 and draw spheres of radius 'cΔt' they are called secondary wavelets.
Draw a surface w2 which is tangential to all these secondary wavelets w2 is the wavefront at time t+Δt Huygen proved the laws of reflection and laws of refraction using concept of wavefront.
Q._E01_078_Q03.png)
Certain plane wavefronts are shown in figure the refractive index of medius is
View Solution_E01_079_Q01.png)
Huygen was the figure scientist who proposed the idea of wave theory of light he said that the light propagates in form of wavelengths. A wavefront is a imaginary surface of every point of which waves are in the same. phase.
For example the wavefront for a point source of light is collection of concentric spheres which have centre at the origin w1 is a wavefront w2 is another wavefront.
The radius of the wavefront at time 't' is 'ct' in thic case where 'c' is the speed of light the direction of propagation of light is perpendicular to the surface of the wavelength. the wavefronts are plane wavefronts in case of a parallel beam of light.
_E01_079_Q02.png)
Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be considered only in the forward direction (i.e., the direction of propagation of light) and not in the reverse direction if a wavefront w1 and draw spheres of radius 'cΔt' they are called secondary wavelets.
Draw a surface w2 which is tangential to all these secondary wavelets w2 is the wavefront at time t+Δt Huygen proved the laws of reflection and laws of refraction using concept of wavefront.
Q. The wavefrot of a light beam is given by the equation x+2y+3z=c (where c is arbitrary constant) then the angle made by the direction of light with the y-axis is
View Solution
