Find the moment of inertia of a uniform cylinder about an axis through its centre of mass and perpendicular to its base. Mass of the cylinder is M and radius is R.
We assume the rotation axis to be transverse axis through the centre of mass of the linear molecule H2. Then each of the hydrogen atom is a distance 12R from the CM. Therefore, the MI of the molecule about this axis, I=2m(R2)2=12mR2.
Topper's Solved these Questions
- VERY SHORT ANSWER QUESTIONS Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:VERY SHORT ANSWER QUESTIONS Exercise:OSCILLATIONS
Explore 11 Videos
- VERY SHORT ANSWER QUESTIONS Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:VERY SHORT ANSWER QUESTIONS Exercise:ELASTICITY
Explore 9 Videos
- VERY SHORT ANSWER QUESTIONS Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:VERY SHORT ANSWER QUESTIONS Exercise:GRAVITATION
Explore 11 Videos
- SOLVED PROBLEMS-II Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SOLVED PROBLEMS-II Exercise:Assignments
Explore 5 Videos
Similar Questions
The moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionFind the moment of inertia of a half uniform ring (mass m, radius r) about its center.
View Solution
Knowledge Check
A uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
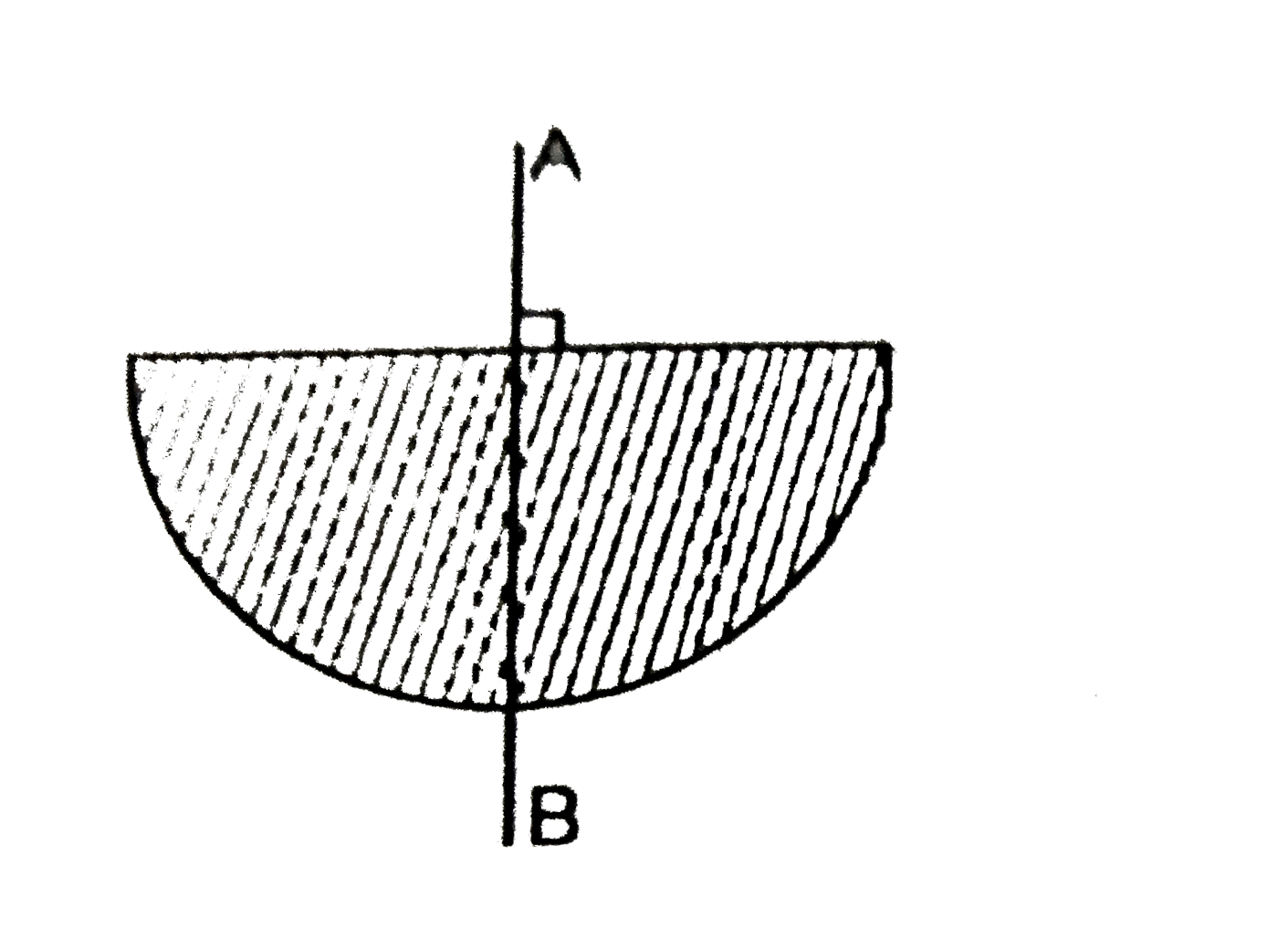 AMR22−M(2Rπ)2BMR22−M(4Rπ)2CMR22+M(4R3π)2DMR22+M(2Rπ)2
AMR22−M(2Rπ)2BMR22−M(4Rπ)2CMR22+M(4R3π)2DMR22+M(2Rπ)2Moment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
AMR22−M(4R3π)2BMR22−M(√24R3π)2CMR22+M(4R3π)2DMR22+M(√24R3π)2The radius of gyration of an uniform rod of length L about an axis passing through its centre of mass and perpendicular to its length is.
AL√2BL2√12CL√3DL√2
The moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionThe moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionThe moment of inertia of a uniform semicircular wire of mass M and radius R about an axis passing through its centre of mass and perpendicular to its plane is xMR210. Find the value of x? (Take π2=10)
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2 R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I, and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2 then
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View Solution

