The maximum value of z=6x+8y subject to x−y≥0,x+3y≤12,x≥0,y≥0 is . . .
A
72
B
42
C
96
D
24
Video Solution
Text Solution
The correct Answer is:A
We have, z=6x+8y
subject to constrants x-y≥0,x+3y≤12,x≥0,y≥0. On taking given constraints as equations,
we get the following graph
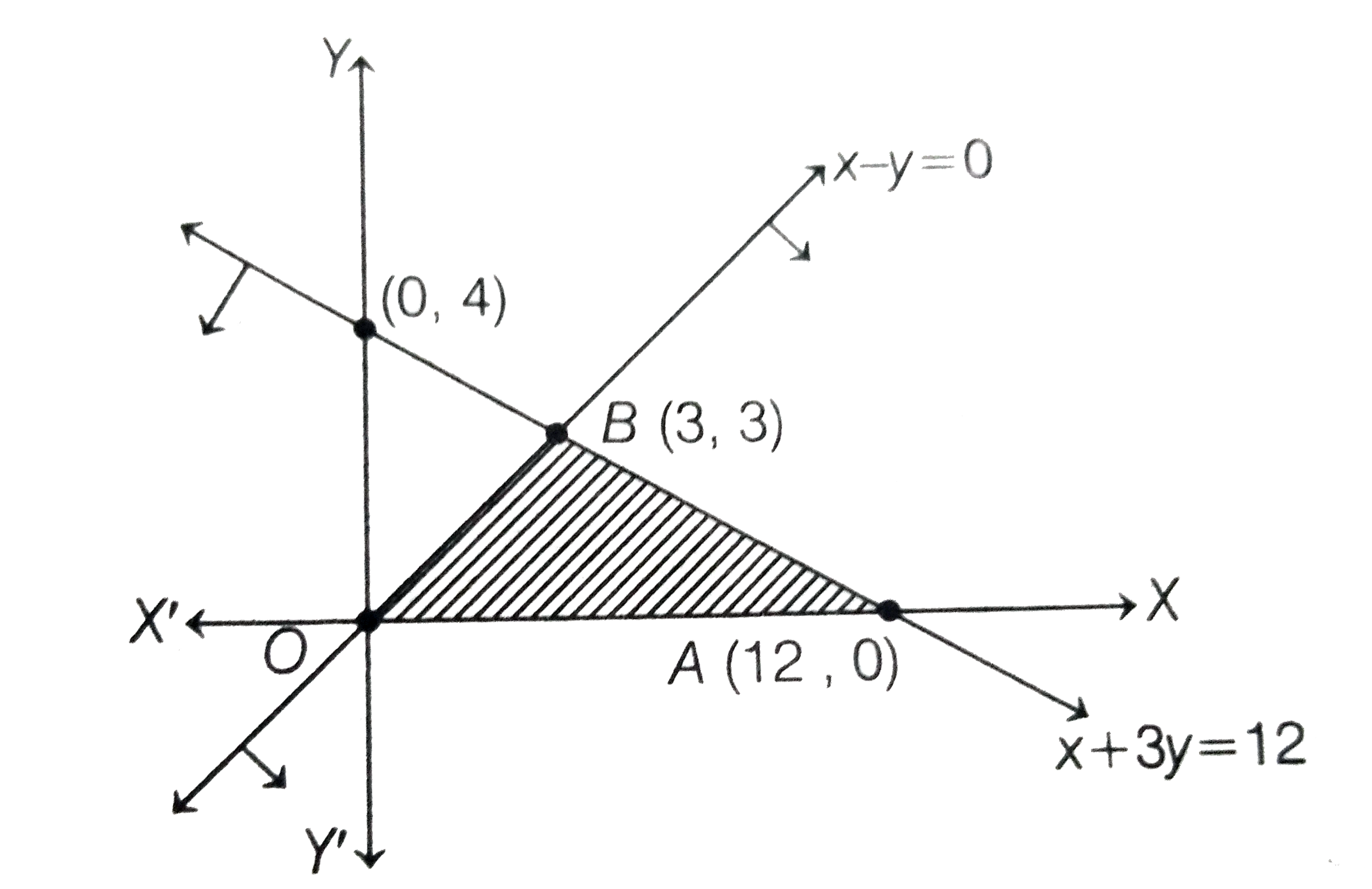
Intersecting point of the line x-y=0 and x+3y=12 is
B(3,3)
Here, OABO is the required feasible region whose corner points are O(0,0),A(12,0) and B(0,4)
Now,
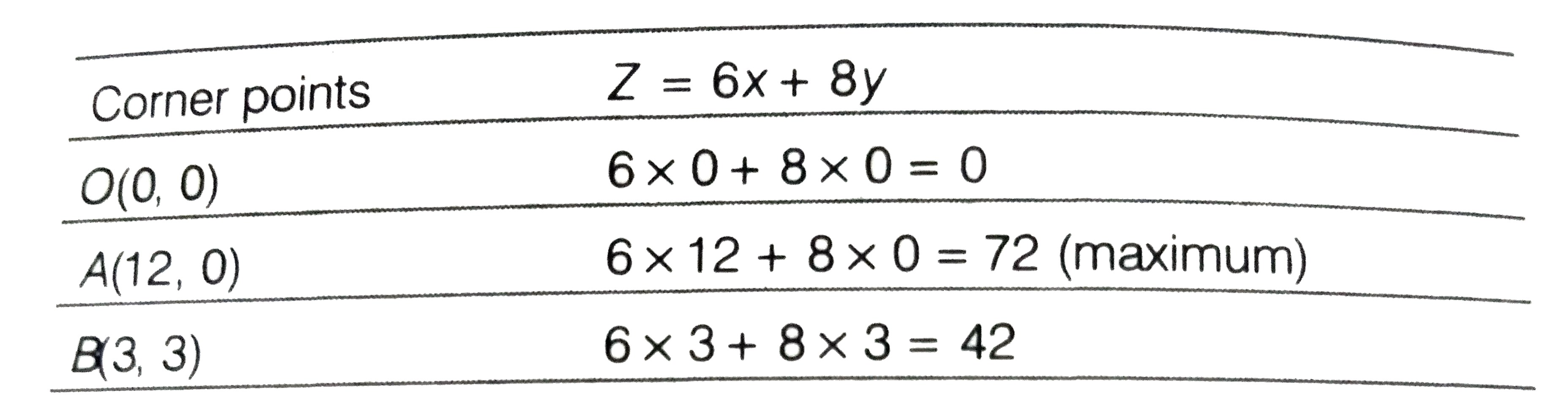
∴Maximum value of Z is 72.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The maximum value of z=15x+30y subject to 3x+y≤12,x+2y≤10,x≥0,y≥0 is
A60B150C160D100The maximum value of z=x+y subject to x+y≤10,3x−2y≤15,x≤6,x≥0,y≥0 is
A5B7.5C12D10The maximum value of z=9x+11y subject to 3x+2y≤12,2x+3y≤12,x≥0,y≥0 is
A44B54C36D48
The maximum value of z=75x+50y subject to 8x+5y≤60,4x+5y≤40,x≥0,y≥0 is
View SolutionThe maximum value of z=7x+11y subject to 3x+5y≤26,5x+3y≤30,x≥0,y≥0, is
View SolutionThe maximum value of z=4x+6y subject to 3x+2y≤12,x+y≥4,x≥0,y≥0 is
View SolutionThe minimum value of z=6x+2y subject to 5x+9y≤90,x+y≥4,y≤8,x≥0,y≥0 is
View SolutionThe maximum value of Z=5x+4y, subject to y≤2x,x≤2y,x+y≤3,x≥0,y≥0 is . . .
View Solution
