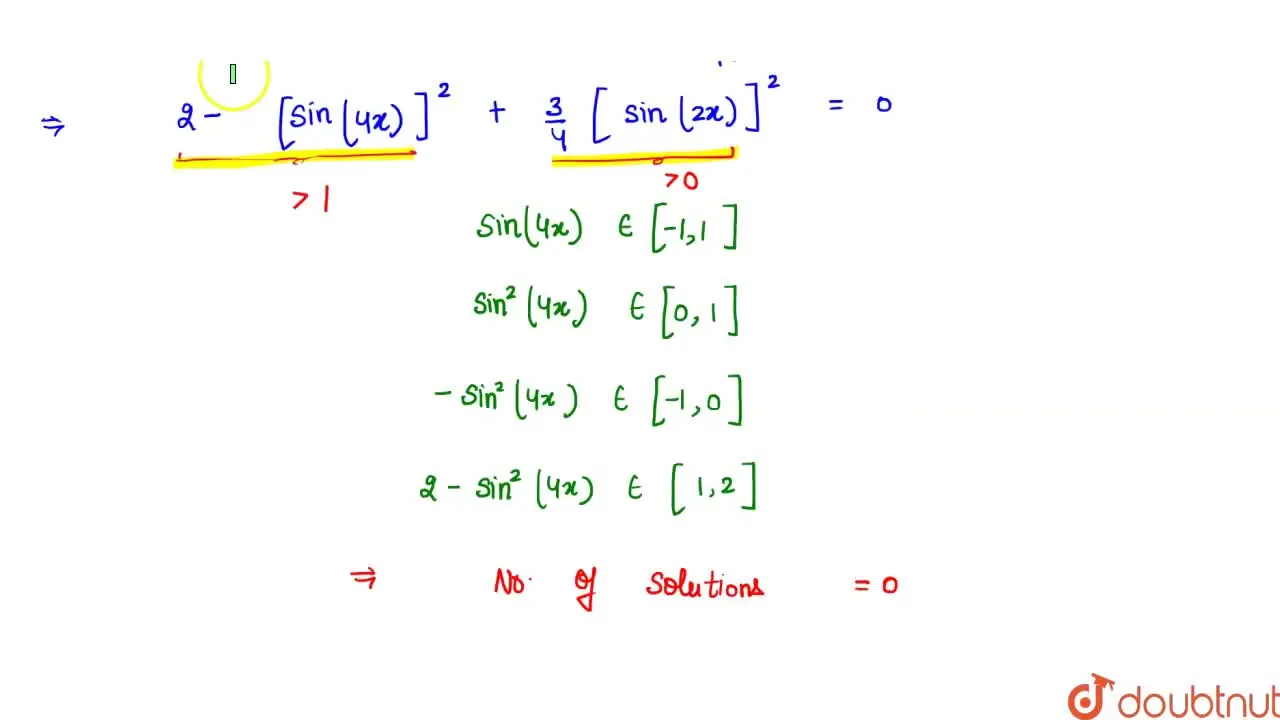The number of solutions of the equation 2(sin42x+cos42x)+3sin2xcos2x=0 is
0
1
2
3
The correct Answer is:A
Step by step video, text & image solution for The number of solutions of the equation 2(sin^(4)2x+cos^(4)2x)+3sin^(2)xcos^(2)x=0 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
Find the number of solutions of the equation sin4x+cos4x−2sin2x+34sin22x=0 in the interval [0,2π]
View SolutionThe number of solutions of the equation sin2x+cos4x=2 is
View SolutionThe number of solution of the equation sin3xcosx+sin2xcos2x+cos3xsinx+1=0 in the interval [0,2π] is equal to
View Solution∫sin42x+cos42xsin22xcos22xdx=
View SolutionNumber of solution(s) of the equation x2+2xcosx=2sinx+3
View SolutionNumber of solutions of the equation sin2x+sin22x−sin23x−sin24x=0lying in the interval (0,π2)]
View SolutionThe total number of solution of the equation sin4x+cos4x=sinxcosx in [0,2π] is :
View SolutionFind the number of solutions of the equation 2sin2x+sin22x=2,sin2x+cos2x=tanx in [0,4π] satisfying the condition 2cos2x+sinx≤2.
View SolutionThe number of solutions to the equations cos4x+1cos2x=sin4x+1sin2x in the interval [0,2π] is
View SolutionThe number of solutions of the equation sin3xcosx+sin2xcos2x+cos3xsinx=1 in the interval [0,2π] is /are
View Solution