For a random variable X, E(X)=3 and E(X2)=11 Then, variance of X is
8
5
2
1
The correct Answer is:C
To find the variance of the random variable X, we can use the formula for variance:
Var(X)=E(X2)−(E(X))2
We are given the following values:
- E(X)=3
- E(X2)=11
Now, let's calculate the variance step by step.
Step 1: Calculate (E(X))2
First, we need to calculate (E(X))2:
(E(X))2=(3)2=9
Step 2: Substitute the values into the variance formula
Now we substitute the values into the variance formula:
Var(X)=E(X2)−(E(X))2=11−9
Step 3: Perform the subtraction
Now, we perform the subtraction:
Var(X)=11−9=2
Conclusion
The variance of the random variable X is:
Var(X)=2
- E(X)=3
- E(X2)=11
First, we need to calculate (E(X))2:
Now we substitute the values into the variance formula:
Now, we perform the subtraction:
The variance of the random variable X is:
Topper's Solved these Questions
- PROBABILITYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PROBABILITYEXERCISE - Exercise 2 (MISCELLANEOUS PROBLEMS)
40 Videos
- PROBABILITYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PROBABILITYEXERCISE - MHT CET Corner
4 Videos
- PROBABILITYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PROBABILITYEXERCISE - PRACTICE EXERCISE (Exercies 2 (MISCELLANEOUS PROBLEMS))
30 Videos
- PRACTICE SET 24BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PRACTICE SET 24EXERCISE - Paper 2 (Mathmatics)
50 Videos
- SEQUENCES AND SERIES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SEQUENCES AND SERIES EXERCISE - EXERCISE 31
1 Videos
Similar Questions
Knowledge Check
For a random variable X, E(X)=3andE(X2)=11. Then, variance X is
A8B5C2D1For a random variable X, if Var (X) = 4 and E(X2)=13, the value of E(X) is
A3B4C5D6For a random variable X, if E(X) = 5 and V(X) = 6, then E(X2) is equal to
A19B31C61D11
For a random variable X, it is given, E(X)=10 and Var(X)=25 . Find the positive values of a and b such,that Y=aX−b have expectation 0 and variance 1.
View SolutionA random variable X has the distribution.
Then , variance of the distribution, is
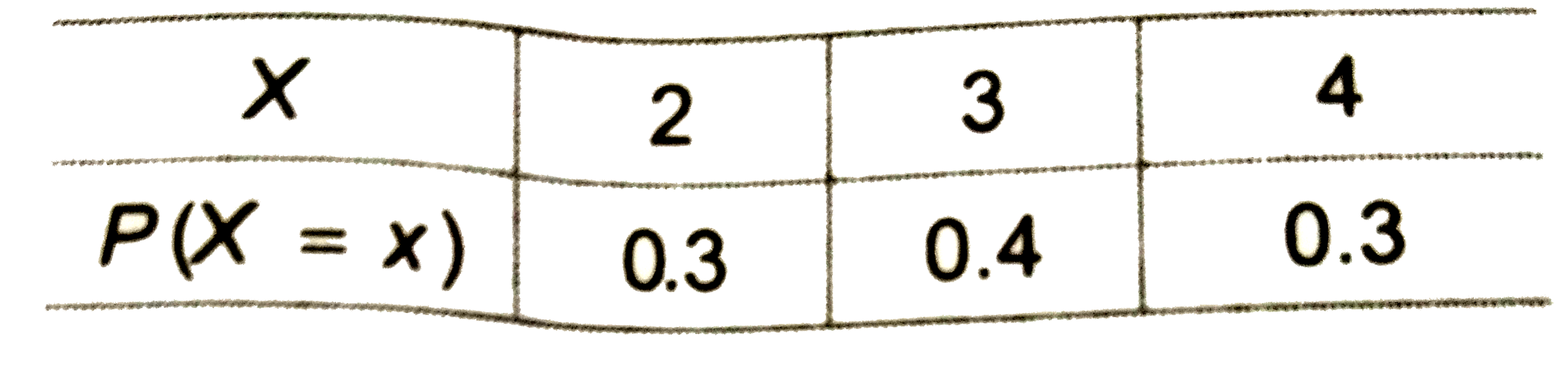
View SolutionIf the probability distribution of a random variable X is as given below
Then, mean and variance are

View SolutionFor the random variable X , if V(X) = 4 , E(X) = 3 , then E(X2) is …
View SolutionFor a random variable X, if E(X2) = 31 , Var(X) = 6, then E(X)=.........
View Solution

