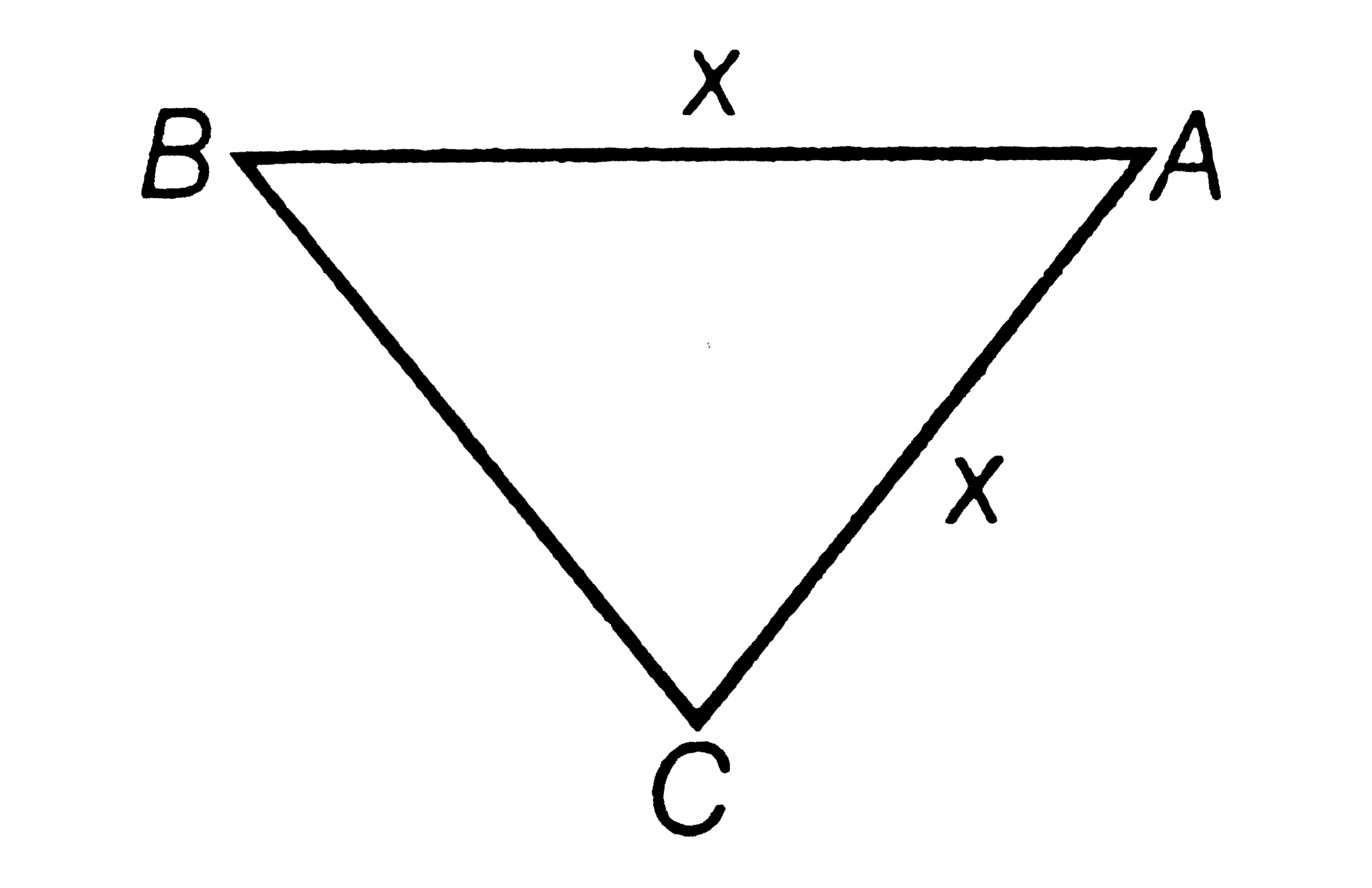
A triangular park is enclosed on two sides by a fence and on the third

A triangular park is enclosed on two sides of a fence and on the third side by a straight river bank. The two sides having fence are of same length x. The maximum area enclosed by the park is
A $\frac{3}{2} x^{2}$
B $\sqrt{\frac{x^{3}}{8}}$
C $\frac{1}{2} x^{2}$
D $π x^{2}$
A triangle park is enclosed on two sides by a fence and, on the third side, by a straight river bank.
If the two fenced side have same length x, then the maximum area of the park is
A $\frac{3}{2} x^{2}$
B $\frac{x \sqrt{x}}{2 \sqrt{2}}$
C $\frac{1}{2} x^{2}$
D $π x^{2}$
The adjacent sides of a rectangle with given perimeter as 100 cm and enclosing maximum area are
A10 cm and 40 cm
B20 cm and 30 cm
C25 cm and 25 cm
D15 cm and 35 cm

A triangular park is enclosed on two sides by a fence and on the third side by a straight river bank. Two having fence are of same length x. The maximum area enclosed by the park is :-