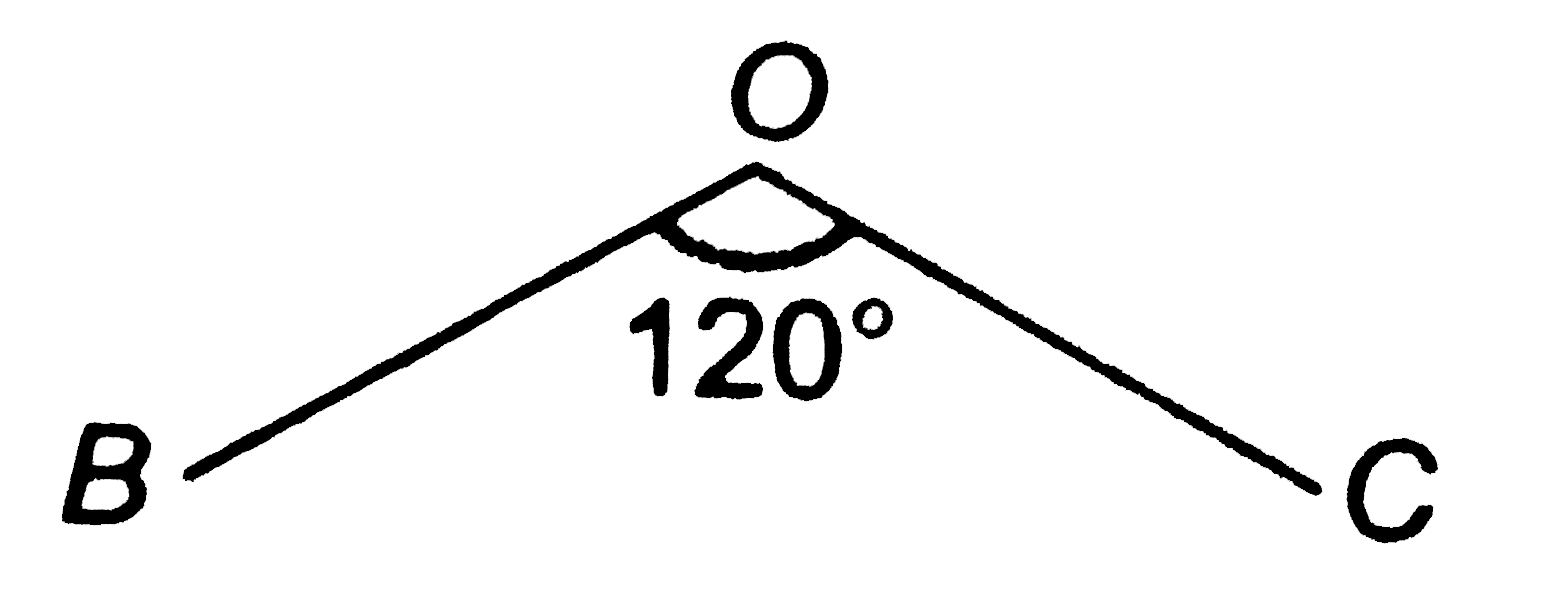
OB and OC are two roads enclosing an angle of $120^{\circ}$ . X and Y start along OB with a speed of $4 k m h^{- 1}$ and Y travels alog OC with a speed of $3 k m h^{- 1}$ . The rate at which the shortest distance between X and Y is increasing after 1h is

A

$\sqrt{37} k m h^{- 1}$

B

$37 k m h^{- 1}$

C

$13 k m h^{- 1}$

D

$\sqrt{13} k m h^{- 1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

After time $t$ the distance covered by $X$ is $4 t$ and $Y$ is $3 t$ .
Let shortest distance between X and Y is A. Then, by cosine law
$A^{2} = {(4 t)}^{2} + {(3 t)}^{2} - (4 t) (3 t) 2 {\cos 120}^{\circ}$
$\Rightarrow A^{2} = 16 t^{2} - 9 t^{2} - 24 t^{2} (- \frac{1}{2}) = 37 t^{2}$ …………….i
$\Rightarrow A = \sqrt{37 t}$
If $t = 1 h,$ then $A = \sqrt{37} k m$
Now, differentiating Eq. (i) w.r.t $t$ we get
$2 AA' = 37 (2 t)$
After $t = 1 h$ , we get
$2 \sqrt{37} A' = 2 (37) \Rightarrow A' = \sqrt{37} k m / h$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The shortest distance between the lines $y - x = 1$ and the curve $x = y^{2}$ is
A $\frac{\sqrt{3}}{4}$
B $\frac{3 \sqrt{2}}{8}$
C $\frac{2 \sqrt{3}}{8}$
D $\frac{3 \sqrt{2}}{5}$
Question 2 - Select One
The shortest distance between the lines $y - x = 1$ and the curve $x = y^{2}$ is
A $\frac{3 \sqrt{2}}{8}$
B $\frac{2 \sqrt{2}}{8}$
C $\frac{3 \sqrt{2}}{5}$
D $\frac{\sqrt{3}}{4}$
Question 3 - Select One
The shortest distance between the lines $y - x = 1$ and the curve $x = y^{2}$ is
A $\frac{2 \sqrt{3}}{8}$
B $\frac{3 \sqrt{2}}{5}$
C $\frac{\sqrt{3}}{2}$
D $\frac{3 \sqrt{2}}{8}$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DERIVATIVES-MISCELLANEOUS PROBLEMS

Home
Ask Doubt
Profile