The function f(x)=(9−x2)2 increases in
A
(−3,0)∪(3,∞)
B
(−∞,−3)∪(3,∞)
C
(−∞,−3)∪(0,3)
D
(−3,3)
Video Solution
Text Solution
The correct Answer is:A
Given f(x)=(9−x2)2
⇒f'(x)=2(9−x2)(−2x)
Now put f'(x)=0
⇒2(9−x2)(−2x)=0
⇒x=0,±3
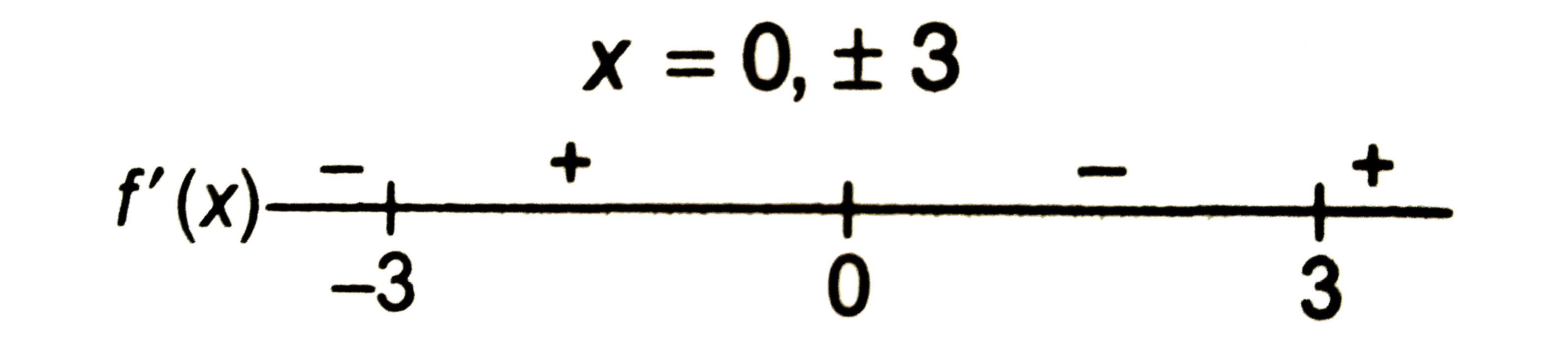
∵f'(x) is increasing in (−3,0)∪(3,∞)
|
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:APPLICATIONS OF DERIVATIVESExercise:MISCELLANEOUS PROBLEMS
Explore 80 Videos
- APPLICATIONS OF DERIVATIVESBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:APPLICATIONS OF DERIVATIVESExercise:MHT CET CORNER
Explore 21 Videos
- APPLICATIONS OF DEFINITE INTEGRALS Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:APPLICATIONS OF DEFINITE INTEGRALS Exercise:MHT CET Corner
Explore 6 Videos
- BINOMIAL DISTRIBUTIONBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:BINOMIAL DISTRIBUTIONExercise:MHT CET Corner
Explore 6 Videos
Similar Questions
Knowledge Check
The interval in which the function f(x)=xe2−x increases is
A(−∞,0)B(2,∞)C(0,2)Dnone of theseWhat is the interval in which the function f(x) =√9−x2 is increasing ? (f(x)>0)
A0<x<3B−3<x<0C0<x<9D−3<x<3The function f(x) =x2−2x increase forall
Ax>−1 onlyBx<=1 onlyCx>1 onlyDx<1 only

