The set of points of discontinuity of the function $f (x) = | sin x |$ is

A

${n π : n \in I}$

B

${(2 n + 1) \frac{π}{2} : n \in I}$

C

$ϕ$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

As tge function | sin x | is defined for all real x.
therefore the function f(x) is continuous for all real x.
Hence, the required set is $ϕ$ (empty set).
Alternate Method

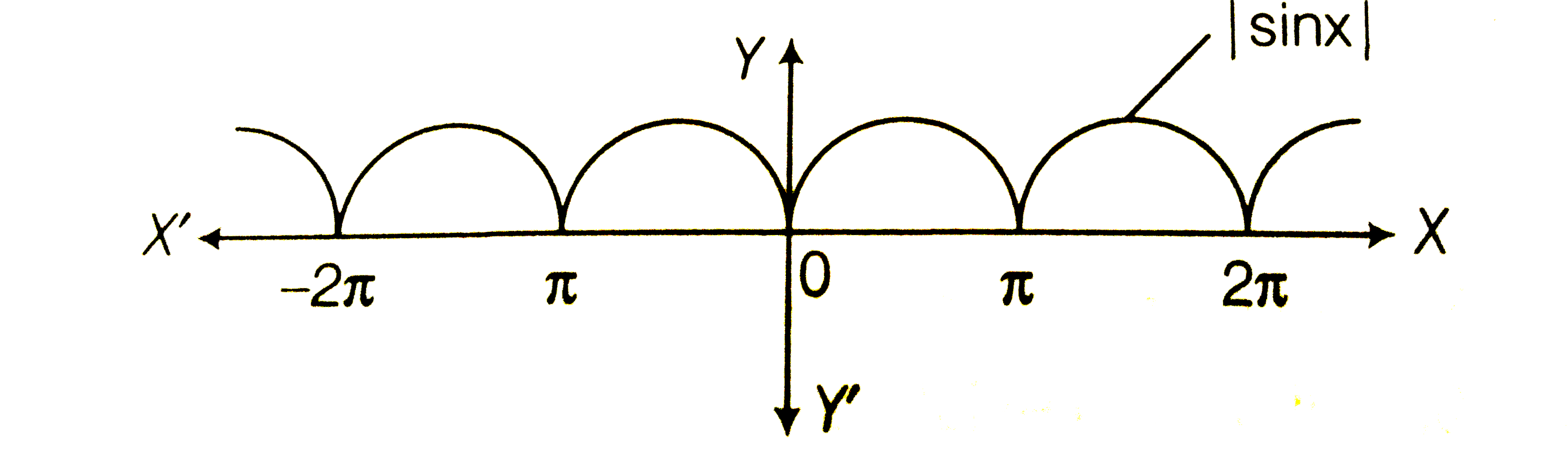
It is clear the figure that there is no break point , so it continuous everywhere.

Updated on:21/07/2023

|

Class 12 MATHS CONTINUITY AND DIFFERENTIABILITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

The set of points of discontinuity of the function $f (x) = log | x |$ is
A{0}
B $ϕ$
C{1, -1}
DNone of these
The set points of discontinuity of the function $f (x) = \frac{| sin x |}{sin x}$ is
A{0}
B ${n π : n \in I}$
C $ϕ$
DNone of these
The set of points of discontinuity of the function $f (x) = \frac{1}{log | x |}, i s$
A{0}
B{-1,1}
C{-1,0,1}
Dnone of these

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-CONTINUITY-MHT CET Corner

Home
Ask Doubt
Profile