The plane 2x+3y+4z=1 meets the coordinate axis in A, B, C. The centroid of the ΔABC is
(2,3,4)
(12,13,14)
(16,19,112)
(12,33,34)
The correct Answer is:C
Given plane can be rewritten as
2x1+3y1+4z1=1
⇒ x12+y13+z14=1
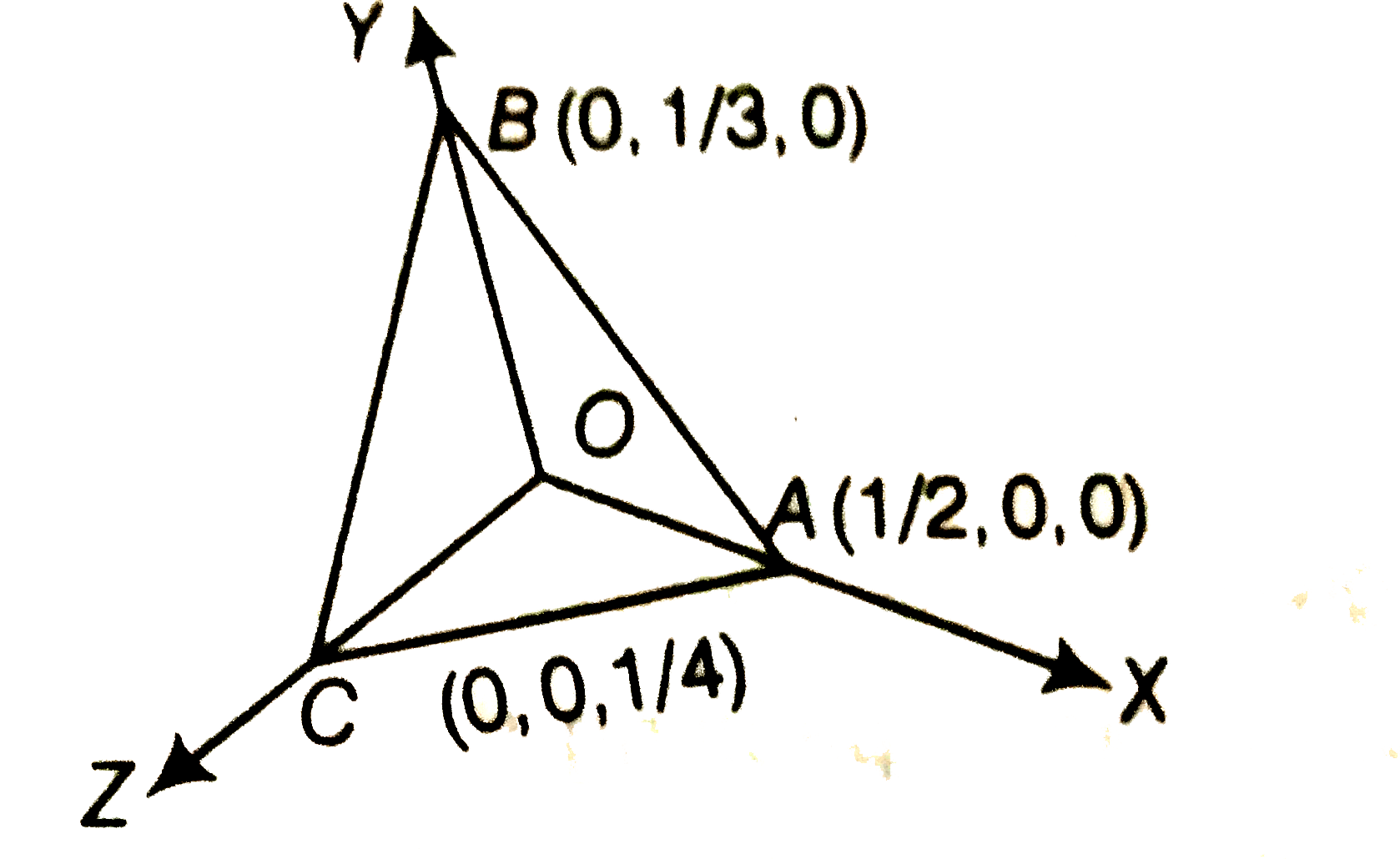
Since, the plane meets the cossdinate axes at
A(12,0,0)B(0,13,0)andC(0,0,14)
then, centroid of the ΔABC
⎛⎝12+0+03,0+13+03,0+0+143⎞⎠
=(16,19,112)
Topper's Solved these Questions
- PLANEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PLANEEXERCISE - MHT CET Corner
9 Videos
- PLANEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PLANEEXERCISE - Practice exercise (Exercise 1) Topical problems (Coplanarity of two lines and distance of a point from a plane)
16 Videos
- PAIR OR STRAIGHT LINES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PAIR OR STRAIGHT LINES EXERCISE - MHT CET Corner
13 Videos
- PRACTICE SET 01BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PRACTICE SET 01EXERCISE - Paper 2 (Mathematics)
50 Videos
Similar Questions
Knowledge Check
The plane 2x+3y+4z=12 meets the coordinate axes in A,B and C. The centroid of △ABC is
A(2,3,4)B(6,4,3)C(2,43,1)Dnone of theseIf the plane 3x−2y−z−18=0 meets the coordinate axes in A,B,C then, the centroid of ΔABC is
A(2,3,-6)B(2,-3,6)C(-2,-3,6)D(2,-3,-6)The plane xa+yb+zc=3 meets the co-ordinate axes in A,B,C. The centroid of the triangle ABC is
A(a3,b3,c3)B(3a,3b,3c)C(1a,1b,1c)D(a,b,c)
A plane P meets the coordinate axes at A B and C respectively . The centroid of ΔABC is give to be (1,1,2) . Then the equation of the line through this centroid and perpendicular to the plane P is ,
View SolutionA plane meets the coordinate axes in points A, B, C and the centroid of the triangle ABC is (α,β,γ). The equation of the plane is
View SolutionThe plane ax+by+cz=l meets the coordinate axes at A,B and C, The centroid of △ABC is
View SolutionA plane meets the coordinate axes at A, B, C such that the centroid of the triangle ABC is at
G(a, b, c). The equation of the plane ABC is
View SolutionA plane a constant distance p from the origin meets the coordinate axes in A, B, C. Locus of the centroid of the triangle ABC is
View Solution
