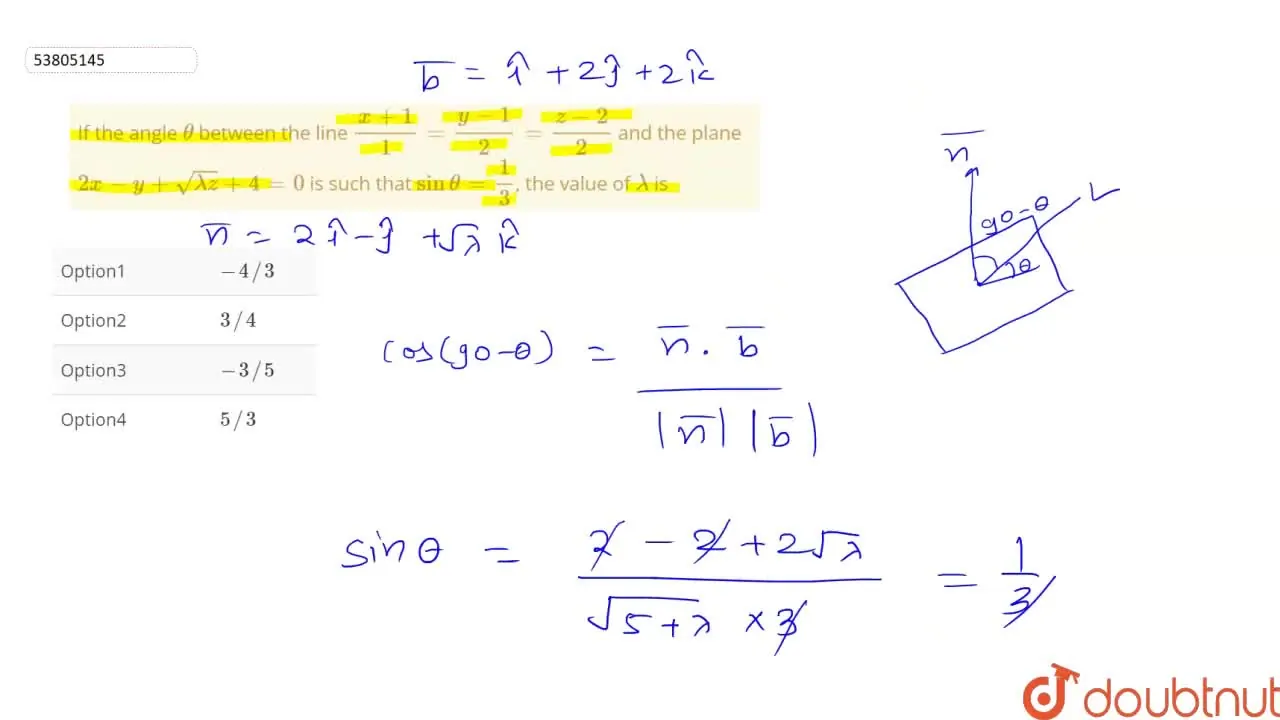
If the angle θ between the line x+11=y−12=z−22 and the plane 2x−y+√λz+4=0 is such that sinθ=13, the value of λ is
−43
34
−35
53
The correct Answer is:D
Here, DR's of line
a1=1,b1=2,c1=2and the plane are a2=2,b2=−1andc2=√λ.
∵sinθ∣∣
∣
∣∣a1a2+b1b2+c1c2√a21+b21+c21√a22+b22+c22∣∣
∣
∣∣
⇒ 13=∣∣∣2−2+2√λ√1+4+4√4+1+λ∣∣∣
⇒√5+λ=2√λ
⇒ λ=53
Related Playlists
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PLANEEXERCISE - Practice exercise (Exercise 1) Topical problems (Coplanarity of two lines and distance of a point from a plane)16videos
PLANE
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PLANEEXERCISE - Practice exercise (Exercise 2) Miscellaneous problems44videos
PLANE
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PLANEEXERCISE - MHT CET Corner9videos
PLANE
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PAIR OR STRAIGHT LINES EXERCISE - MHT CET Corner13videos
PAIR OR STRAIGHT LINES
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PRACTICE SET 01EXERCISE - Paper 2 (Mathematics)50videos
PRACTICE SET 01
Similar Questions
If the angle θ between the line x+11=y−12=z−22 and the plane 2x−y+√λz+4=0 is such that sinθ=13. Then, the value of λ is
View SolutionIf the angle θ between the line x+11=y−12=z−22 and the plane 2x−y+√λz+4=0 is such that sinθ=13 then the value of λ is (A) −43 (B) 43 (C) −35 (D) 53
View SolutionIf the angle θ between the line x+11=y−12=z−22 and the plane 2x−y+√λz+4=0 is such that sinθ=13, the value of λ is
View SolutionIf the angle θ between the line x+11=y−12=z−22 and the plane 2x−y+√λz+4=0 is such that sinθ=13. The value of λ is
View SolutionIf angle θ bertween the line x+11=y−12=z−22 and the plane 2x−y+√λz+4=0 is such that s∫hη=1/3, the value of λ is a. −35 b. 53 c. −43 d. 34
View SolutionIf the angle θ between the line x+11=y−12=z−22 and the plane 2x−y+√pz+4=0 is such that sinθ=13, then the values of p is (A) 0 (B) 13 (C) 23 (D) 53
View SolutionIf the angle θ between the line x+11=y−12=z−22 and the plane 2x−y+√λz+4=0 is such that sinθ=13 ,if λ=mn then m+n is (m,n) are relatively prime)
View SolutionFind the angle between line x+13=y−12=z−24 and the plane 2x+y−3z+4=0.
View SolutionThe angle between the line x+13=y−12=z−24 and the plane 2x+y−3z+4=0 is such that sinθ=13, then the value of θ is :
View SolutionIf θ is the angle between the line x+11=y−12=z−22 and the plane
2x−y+√λz+4=0 such that cos θ = 13, then λ is equal toView Solution