A pair of perpendicular straight lines is drawn through the origin forming with the line 2x+3y=6 an isosceles triangle right-angled at the origin. The equation to the line pair is 5x2−24xy−5y2=0 5x2−26xy−5y2=0 5x2+24xy−5y2=0 5x2+26xy−5y2=0
5x2−24xy−5y2=0
5x2−26xy−5y2=0
5x2+24xy−5y2=0
5x2+26xy−5y2=0
The correct Answer is:A
Given line is 2x+3y=6tan45∘∣∣
∣
∣∣m−(−23)1+m−23∣∣
∣
∣∣⇒∣∣∣1−23m∣∣∣=∣∣∣3m+22∣∣∣
⇒3−2m=±(3m+2)
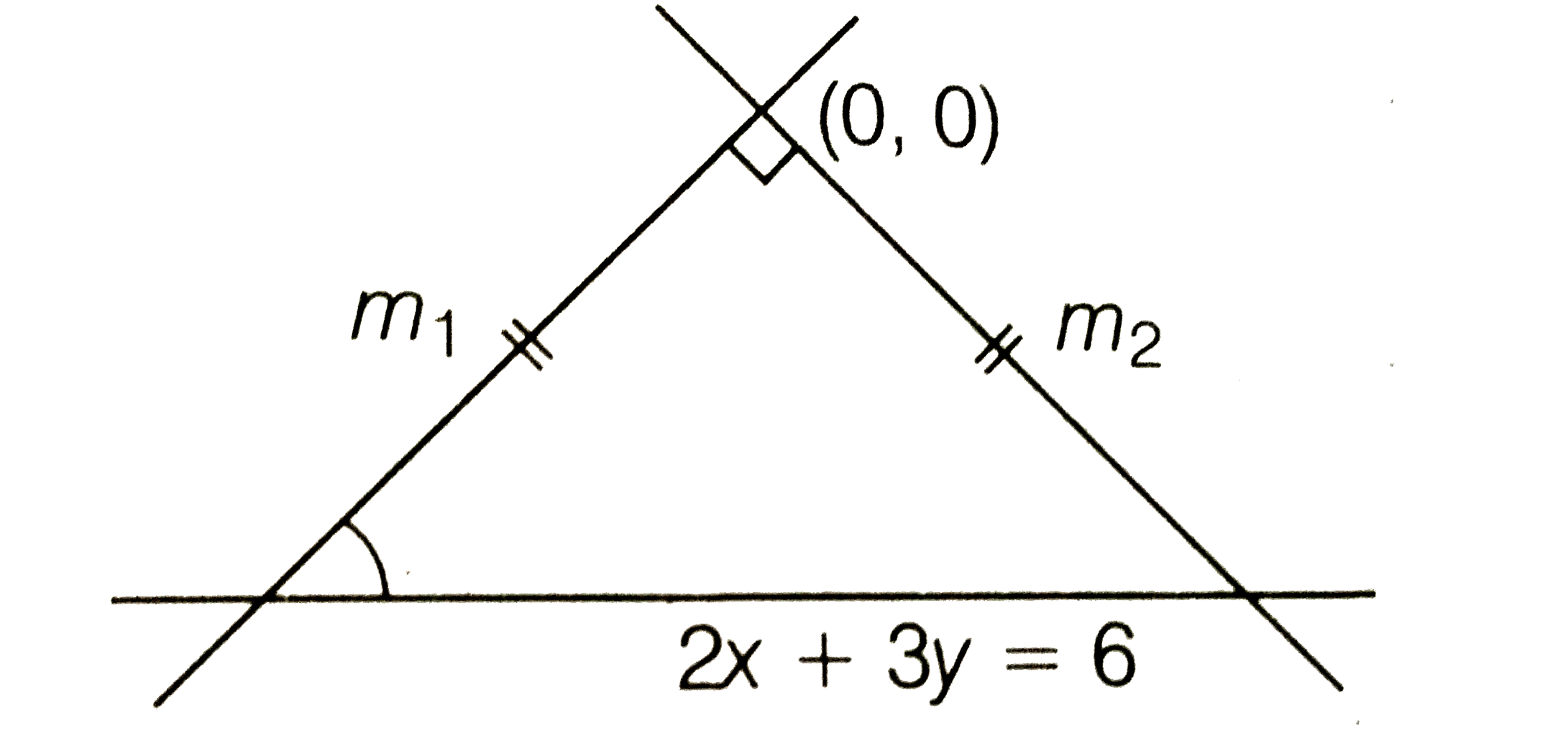
Hence , m1=−5,m2=1/5
Hence , lines are y=−5xandy=x5
∴5x2−24xy−5y2=0 .
Topper's Solved these Questions
- PAIR OR STRAIGHT LINES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PAIR OR STRAIGHT LINES EXERCISE - MHT CET Corner
13 Videos
- PAIR OR STRAIGHT LINES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PAIR OR STRAIGHT LINES EXERCISE - PRACTICE EXCERCISE (Excercise 1) (Topical Problems) (General Equation of Second Degree)
20 Videos
- MOCK TEST 5BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MOCK TEST 5EXERCISE - MCQS
50 Videos
- PLANEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PLANEEXERCISE - MHT CET Corner
9 Videos
Similar Questions
A pair of perpendicular straight lines is drawn through the origin forming with the line 2x+3y=6 an isosceles triangle right-angled at the origin. The equation to the line pair is 5x2−24xy−5y2=0 5x2−26xy−5y2=0 5x2+24xy−5y2=0 5x2+26xy−5y2=0
View SolutionThe equation of the line through the intersection of the lines 2x−3y=0 and 4x−5y=2 and

View Solution
Knowledge Check
The joints equation of the lines 3x−2y+5=0and5x−3y=0 is
A15x2−19xy+6y2−25x−15y=0B15x2−19xy+6y2+25x−15y=0C15x2−xy+6y2+25x−15y=0D15x2+xy+6y2+25x−15y=0The equation of the line joining the origin to the point of intersection of the lines 2x2+xy−y2+5x−y+2=0 is
Ax+y=0Bx-y=0Cx-2y=0D2x+y=0
The equation of the straight line through the point of intersection of lines x-3y+1=0 and 2x+5y-9=0 and whose distance from the origin is 5
View SolutionThe equation of the straight line through the point of intersection of lines x−3y+1=0 and 2x+5y−9=0 and whose distance from the origin is √5 is
View SolutionThe acute angle between the lines (5x−2y)2−3(2x+5y)2=0 is
View SolutionFouation of the pair of straight lines through origin and perpendicular to the pair of straight lines 5x2−7xy−3y2=0 is
View SolutionJoint equation of two lines through the origin and parallel to the pair of lines 2x2−xy−y2+5x+y+2=0 is
View SolutionFind the equation of a straight line through the point of intersection of the lines 4x−3y=0 and 2x−5y+3=0 and parallel to 4x+5y+6=0.
View Solution
