If the angles of a triangle are in the ratio $4 : 1 : 1,$ then the ratio of the longest side to the perimeter is $\sqrt{3} : (2 + \sqrt{3})$ (b) $1 : 6$ $1 : 2 + \sqrt{3}$ (d) $2 : 3$

A

$\sqrt{3} : (2 + \sqrt{3})$

B

$1 : 6$

C

$1 : (2 + \sqrt{3})$

D

$2 : 3$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Here , ratio of angles are $4 : 1 : 1$ .
$\Rightarrow 4 x + x + x = 180^{\circ}$
$\Rightarrow x = 30^{\circ}$
$∴ ∠ A = 120^{\circ}, ∠ B = ∠ C = 30^{\circ}$

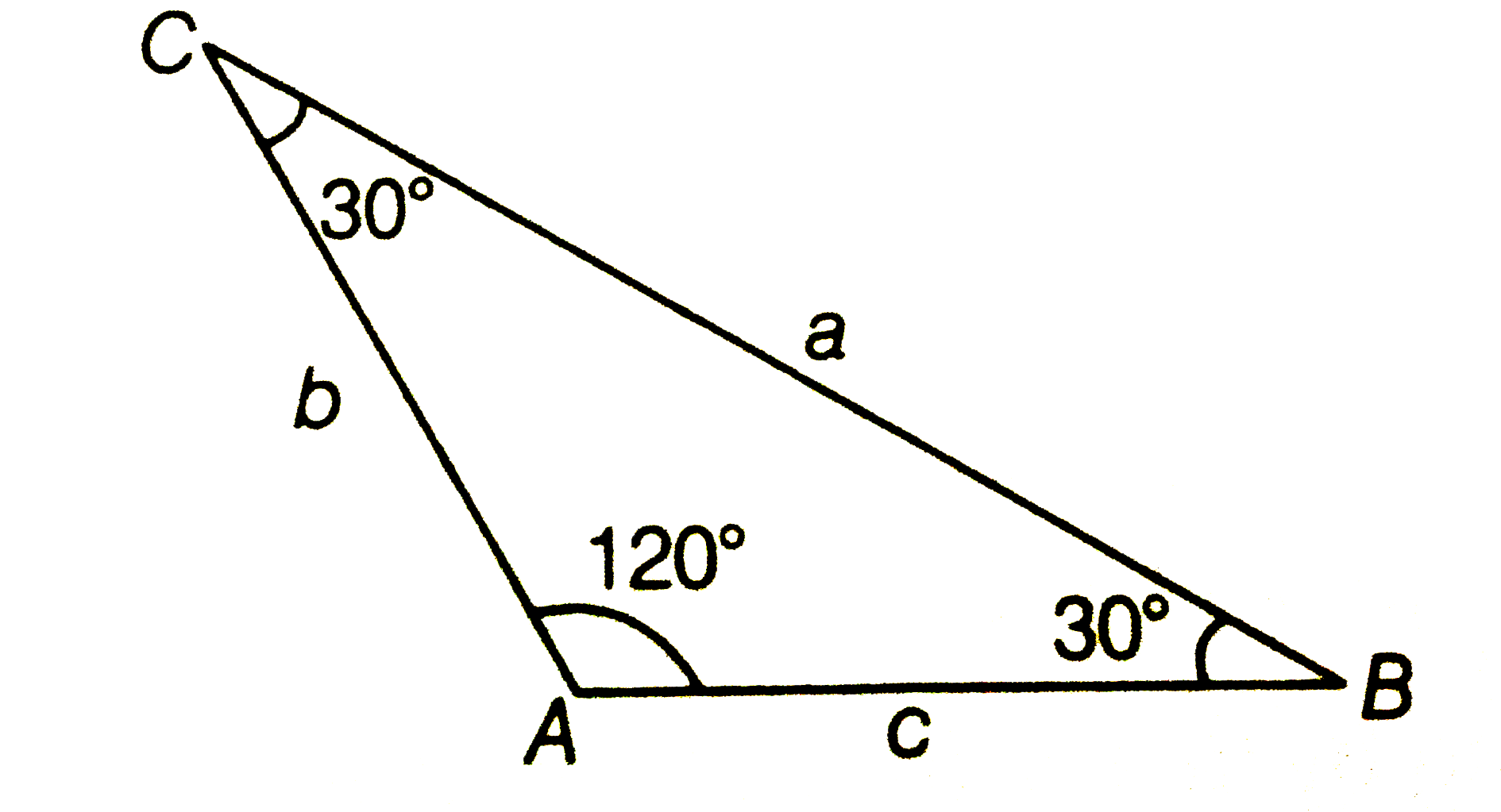
Thus ,the ratio of longest side to the perimeter $= \frac{a}{a + b + c}$ Let b = c =x
$∴ a^{2} = b^{2} + c^{2} - 2 b c cos A$
$\Rightarrow a^{2} = 2 x^{2} - 2 x^{2} cos A = 2 x^{2} (1 - cos A)$
$\Rightarrow a^{2} = 4 x^{2} {sin}^{2} \frac{A}{2}$
$\Rightarrow a = 2 x sin \frac{A}{2}$
$\Rightarrow a = 2 x {sin 60}^{\circ} = \sqrt{3} x$
Thus ,required ratio is
$\frac{a}{a + b + c} = \frac{\sqrt{3} x}{x + x + \sqrt{3} x} = \frac{\sqrt{3}}{2 + \sqrt{3}}$

|

Updated on:21/07/2023

Class 12 MATHS TRIGONOMETRIC FUNCTIONS

Similar Questions

Knowledge Check

Question 1 - Select One
The angles of a triangle are in the ratio $4 : 1 : 1$ . Then the ratio of the largest side to the perimeter is
A $\sqrt{3} : (2 + \sqrt{3})$
B $1 : 6$
C $1 : 2 + \sqrt{3}$
D $2 : 3$
Question 2 - Select One
If the angles of the triangle are in the ratio $4 : 1 : 1$ , then the ratio of the longest side to the perimeter is
A $\sqrt{3} : (2 + \sqrt{3})$
B $1 : 6$
C $1 : 2 + \sqrt{3}$
D $2 : 3$
Question 3 - Select One
If the angles of a triangle are in the ratio $4 : 1 : 1$ , then the ratio of the longest side to the perimeter is
A $2 \sqrt{3} - 3$
B $2 \sqrt{3} + 3$
C $3 \sqrt{2} + 3$
D $3 \sqrt{2} + 2$

Recommended Questions

Home
Ask Doubt
Profile