If for the reaction A→B rate=−d[A]dt=2d[B]dt then, rate law is
−d[A]dt=k[A]2
d[B]dt=k[A]
d[A]dt=k[A]2
−d[B]dt=k[B]2
The correct Answer is:A
To derive the rate law for the reaction A→B given the relationship between the rates of change of concentrations, we can follow these steps:
Step 1: Understand the given relationship
The problem states that:
−d(A)dt=2d(B)dt
This indicates how the concentration of A decreases relative to the concentration of B increases.
Step 2: Express the rate in terms of concentration
From the relationship, we can express the rate of the reaction in terms of the concentration of A:
−d(A)dt=2d(B)dt
This implies that for every 1 mole of A that reacts, 2 moles of B are produced.
Step 3: Define the rate law
The general form of the rate law for a reaction is given by:
Rate=k(A)n
where k is the rate constant, (A) is the concentration of the reactant, and n is the order of the reaction with respect to A.
Step 4: Determine the order of the reaction
From the stoichiometry of the reaction, we see that the rate of disappearance of A is twice the rate of formation of B. This suggests that the reaction is first order with respect to A, but since the stoichiometry shows that 2 moles of B are produced for every mole of A consumed, we can infer that the order of the reaction is 2 with respect to A.
Step 5: Write the final rate law expression
Thus, the rate law can be expressed as:
Rate=k(A)2
Summary
The rate law for the reaction A→B is:
Rate=k(A)2
The problem states that:
−d(A)dt=2d(B)dt
This indicates how the concentration of A decreases relative to the concentration of B increases.
From the relationship, we can express the rate of the reaction in terms of the concentration of A:
−d(A)dt=2d(B)dt
This implies that for every 1 mole of A that reacts, 2 moles of B are produced.
The general form of the rate law for a reaction is given by:
Rate=k(A)n
where k is the rate constant, (A) is the concentration of the reactant, and n is the order of the reaction with respect to A.
From the stoichiometry of the reaction, we see that the rate of disappearance of A is twice the rate of formation of B. This suggests that the reaction is first order with respect to A, but since the stoichiometry shows that 2 moles of B are produced for every mole of A consumed, we can infer that the order of the reaction is 2 with respect to A.
Thus, the rate law can be expressed as:
Rate=k(A)2
The rate law for the reaction A→B is:
Rate=k(A)2
Topper's Solved these Questions
Similar Questions
The rate law equation for the reaction A→B is found to be −d[A]dt=k[A]1/2
If [A]0 were the initial concentration of A, derive expressions for
(i) rate constant in the integrated form (ii) half-life period of the reaction
View SolutionFor the reaction ,XA+YB→ZC
If −d[A]dt=−d[B]dt=1.5d[C]dt. then the correct statements among the following is:
View Solution
Knowledge Check
In the reaction xA→yB,log{−d[A]dt}=log{+d[B]dt}+0.3 Then, x:y is
A2:1B1:2C3:1D3:10The rate and mechamical reaction are studied in chemical kinetics. The elementary reactions are single step reaction having no mechanism. The order of reaction and molecularity are same for elementary reactions. The rate of forward reaction aA+bB→cC+dD is given as:
rate=(dxdt)=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt or expression can be written as : rate =K1[A]a[B]b−K2[C]c[D]d. At equilibrium, rate =0. The constants K,K1,K2 are rate constants of respective reaction. In case of reactions governed by two or more steps reaction mechanism, the rate is given by the slowest step of mechanism.
For the reaction, aA→bB,
log[−dAdt]=log[dBdt]+0.6, then a:b is:A(a) 3.98B(b) 2.18C(c ) 1.48D(d) 0For the reaction aA+bB→cC, if −3d[A]dt=−d[B]dt=+1.5d[C]dt, then a, b and c respectively are
A3,1,2B2,1,3C1,3,2D6,2,3
For the reaction ,XA+YB→ZC
If −d[A]dt=−d[B]dt=1.5d[C]dt. then the correct statements among the following is:
View SolutionIn the reaction 3A→2B, rate of reaction +d[B]dt is equal to :
View SolutionThe initial rate, −d[A]dt at t=o was found to be 2.6×102 mol L−1s_1 for the reaction
A+2B→products
The initial rate, −d[B]dt, at t=o is
View SolutionFor the reaction
2HX→H2+X2
−d[HX]dt = rate
View SolutionFor the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
A reaction follows the given concentration-time graph. The rate for this reaction at 20s will be
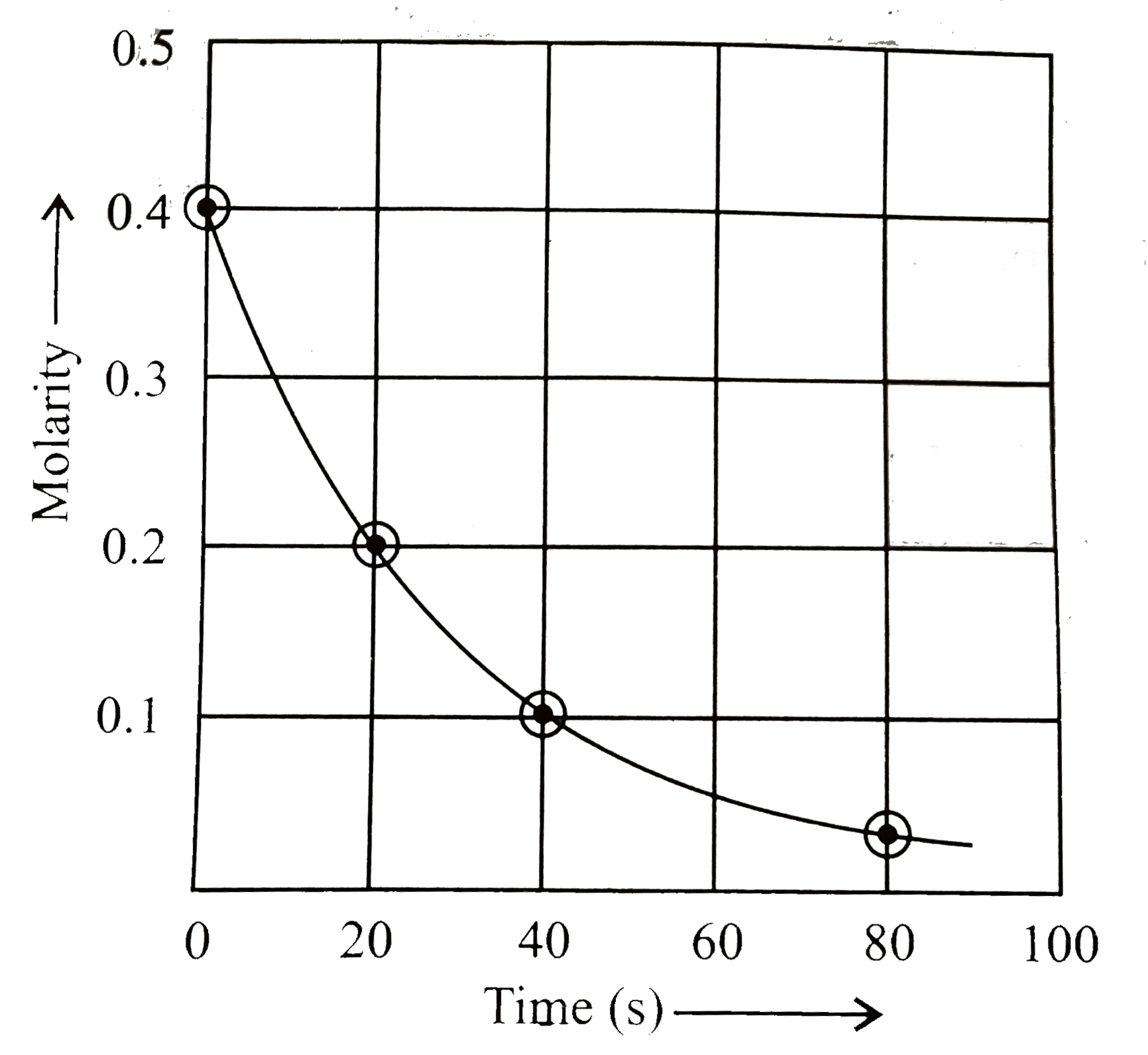
View Solution
