Question

Let $P(-1,0),Q(0,0),R(3,3\sqrt{3})$ be three points then the equation of the bisector of the angle $\angle PQR$ is :

Options

A. `sqrt(3)x+y=0`
B. `x+(sqrt(3))/(2)y=0`
C. `(sqrt(3))/(2)x+y=0`
D. `x+sqrt(3)y=0`

Answer

A

Explanation

Now, slope of
`QR=(3sqrt(3)-0)/(3-0)=sqrt(3)=tantheta`
`implies" "theta=(pi)/(3)`

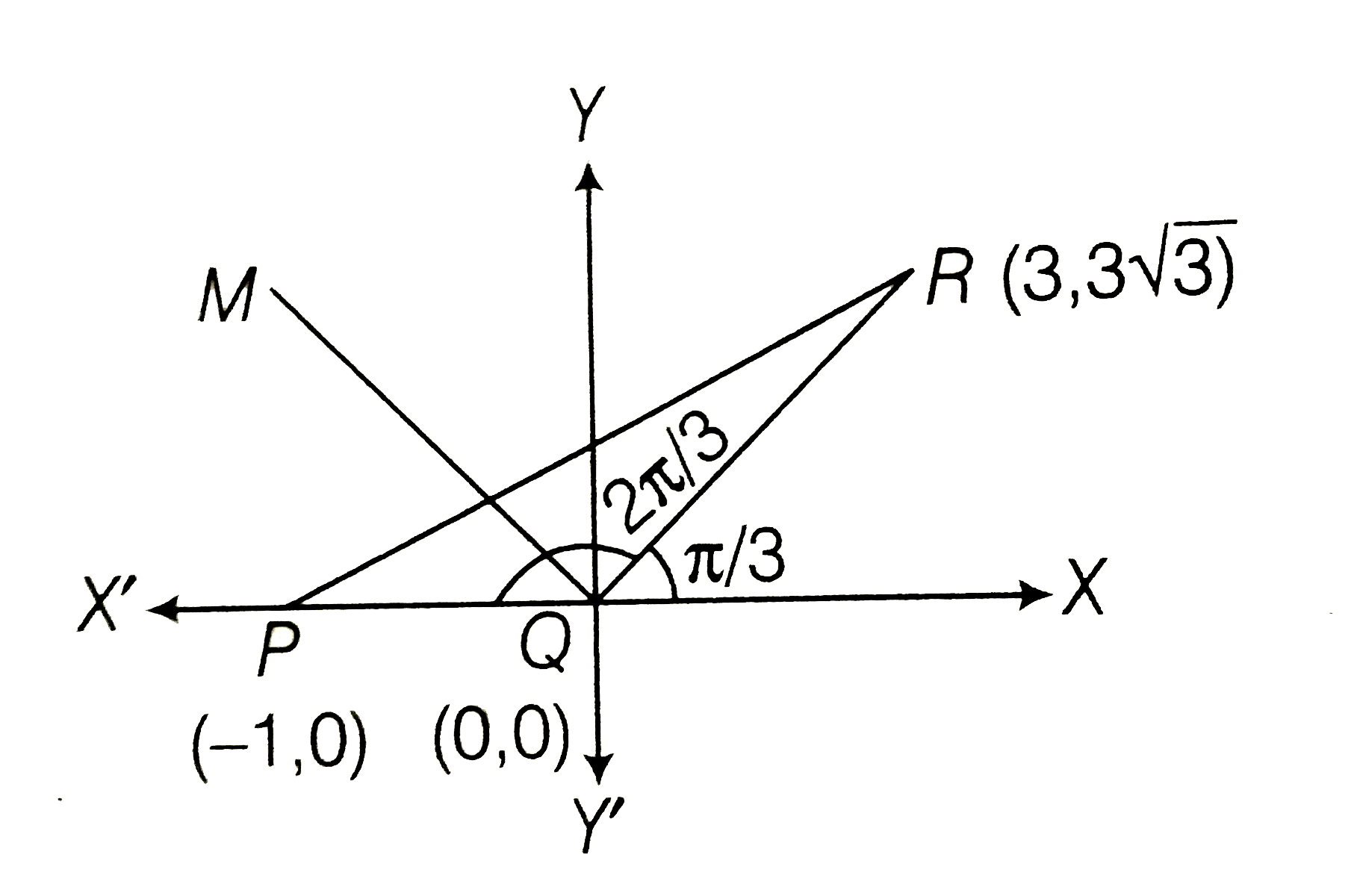
The angle between PQR is `(2pi)/(3)` , so the line QM makes an angle `(2pi)/(3)` from positive direction of X-axis. Slope of the line
`QM=tan""(2pi)/(3)=-sqrt(3)`
Hence, equation of line QM is
`y=-sqrt(3)x`
`impliessqrt(3)x+y=0`