Find the area of the closed figure bounded by the curves y=√x,y=√4−3xandy=0
A
4/9
B
44052
C
16/9
D
none of these
Video Solution
Text Solution
The correct Answer is:B
C1:y=√x
⇒y2=x,y>0
C2:y=√4−3x
⇒y2=3(x−4/3),y>0
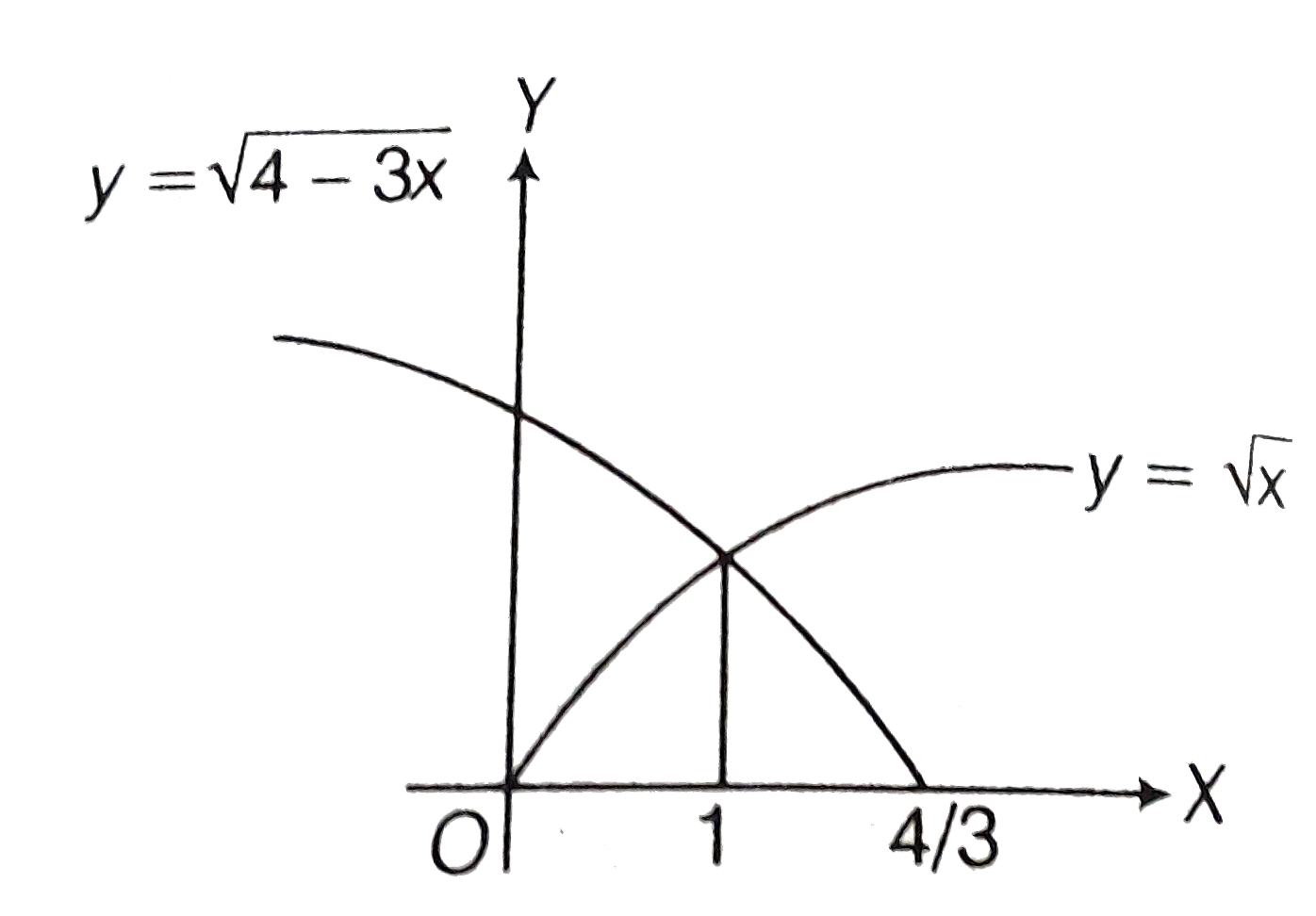
Area=∫10√xdx+∫4/31√4−3xdx=89
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The area of the closed figure bounded by the curves
y=cosx,y=1+2πxandx=π/2, isAπ+44B3π−44C3π4Dπ4The area bounded by the curves y=−√−x and x=−√−y where x,y≤0
Acannot be determinedBis 13Cis 23Dis same as that of the figure bounded by the curves y=√−x,x≤0andx=√−y,y≤0
Find the area of the region bounded by the curve y=x3,y=x+6 and x=0
View SolutionFind the area of the region bounded by the curves y=√x+2andy=1x+1 between the lines x=0 and x=2.
View SolutionFind the area of the region bounded by the curves 2y2=x,3y2=x+1,y=0.
View SolutionFind the area of the region bounded by the curves x2+y2=4, y=√3x and x-axis in the first quadrant.
View SolutionFind the area of the figure bounded by the curve y=sin−1x, the lines x=0 and y=π2.
View SolutionUsing integration find the area of the region bounded by the curves y=√4−x2,x2+y2−4x=0 and the x-axis.
View Solution