Radius of one arm of hyddraulic lift is foud times off radius of other arm. What force should be applied on narrow arm to lift 100 kg?
26.5 N
62.5 N
6.25 N
8.3 N
The correct Answer is:B
To solve the problem, we will use the principle of hydraulic lifts, which states that the pressure applied on one side of the lift is equal to the pressure on the other side.
1. Identify the Radii:
- Let the radius of the narrow arm (r1) be r.
- Then, the radius of the wider arm (r2) is 4r (since it is four times the radius of the narrow arm).
2. Calculate the Areas:
- The area of the narrow arm (A1) is given by:
A1=πr21=πr2
- The area of the wider arm (A2) is given by:
A2=πr22=π(4r)2=π⋅16r2
3. Set Up the Pressure Equation:
- According to the principle of hydraulics, the pressure on both sides must be equal:
FA1=FliftA2
- Here, F is the force applied on the narrow arm, and Flift is the weight being lifted (which is 100 kg).
4. Convert Weight to Force:
- The weight Flift can be calculated as:
Flift=m⋅g=100kg⋅9.8m/s2=980N
5. Substitute Areas into the Pressure Equation:
- Substitute A1 and A2 into the pressure equation:
Fπr2=980π⋅16r2
6. Cancel Common Terms:
- The π and r2 terms cancel out:
F=98016
7. Calculate the Force:
- Now, calculate F:
F=98016=61.25N
Final Result:
The force that should be applied on the narrow arm to lift 100 kg is approximately 61.25 N.
- Let the radius of the narrow arm (r1) be r.
- Then, the radius of the wider arm (r2) is 4r (since it is four times the radius of the narrow arm).
- The area of the narrow arm (A1) is given by:
A1=πr21=πr2
- The area of the wider arm (A2) is given by:
A2=πr22=π(4r)2=π⋅16r2
- According to the principle of hydraulics, the pressure on both sides must be equal:
FA1=FliftA2
- Here, F is the force applied on the narrow arm, and Flift is the weight being lifted (which is 100 kg).
- The weight Flift can be calculated as:
Flift=m⋅g=100kg⋅9.8m/s2=980N
- Substitute A1 and A2 into the pressure equation:
Fπr2=980π⋅16r2
- The π and r2 terms cancel out:
F=98016
- Now, calculate F:
F=98016=61.25N
The force that should be applied on the narrow arm to lift 100 kg is approximately 61.25 N.
Topper's Solved these Questions
Similar Questions
The area of cross section of the two arms of a hydraulilc press are 1 cm^2 and 10 cm^2 respectively figure. A force of 5N is applied on the water in the thinner arm. What force should be applied on the water in the thicker arm so that the water may remain in equilibrium?
 ,
,
View SolutionThe area of cross section of the two arms of a hydraulic press is 1cm2 and 20cm2 respectively. A force of 10N is applied on the water in the thinner arm. What force should be applied on the water in the thicker arms so that water may remain in equilibrium?

View Solution
Knowledge Check
The radius of one arm of a hydraulic lift is three times the radius of the other arm. What force should be applied on the narrow arm so as to lift 50 kg at the wider arm?
A60 NB54.4 NC26.7 ND30 NA ring of radius r, and weight W is lying on a liquid surface . If the surface tension of the liquid is T , then the minimum force required to be applied in order to lift the ring up
AWB2WCW+4πrTDW+2πrT
In a wheel and axle, for one complete rotation the magnitude of displacement of effort is 5 times that of the load. What load can be lifted by applying an effort of 10 N? If the radius of the wheel is 35 cm, what is the radius of the axle?
View SolutionA disc of mass m2 is placed on a table. A stiff spring is attached to it and is vertical. The other end of the spring is attached to a disc of mass m1 What minimum force should be applied to the upper disc to press the spring such that the lower disc is lifted off the table when the external force is suddenly removed?

View SolutionA flywheel of mass 25 kg has a radius of 0.2 m. What force should be applied tangentially to the rim of the flywheel so that it acquires an angular acceleration of 2rad s−2 ?
View SolutionThe average mass that must be lifted by a hydraulic press is 80kg.If the radius of the larger piston is five times that of the smaller piston, what is the minimum force that must be applied?
View SolutionTwo disks of masses m1 and m2 are connected by a spring of force canstant k. The lower disk of mass m2lies on a table and the upper disk is vertically above it. What vertical force F should be applied to the upper disk so that when the force is withdraw, the lower disk is lifted off the table?
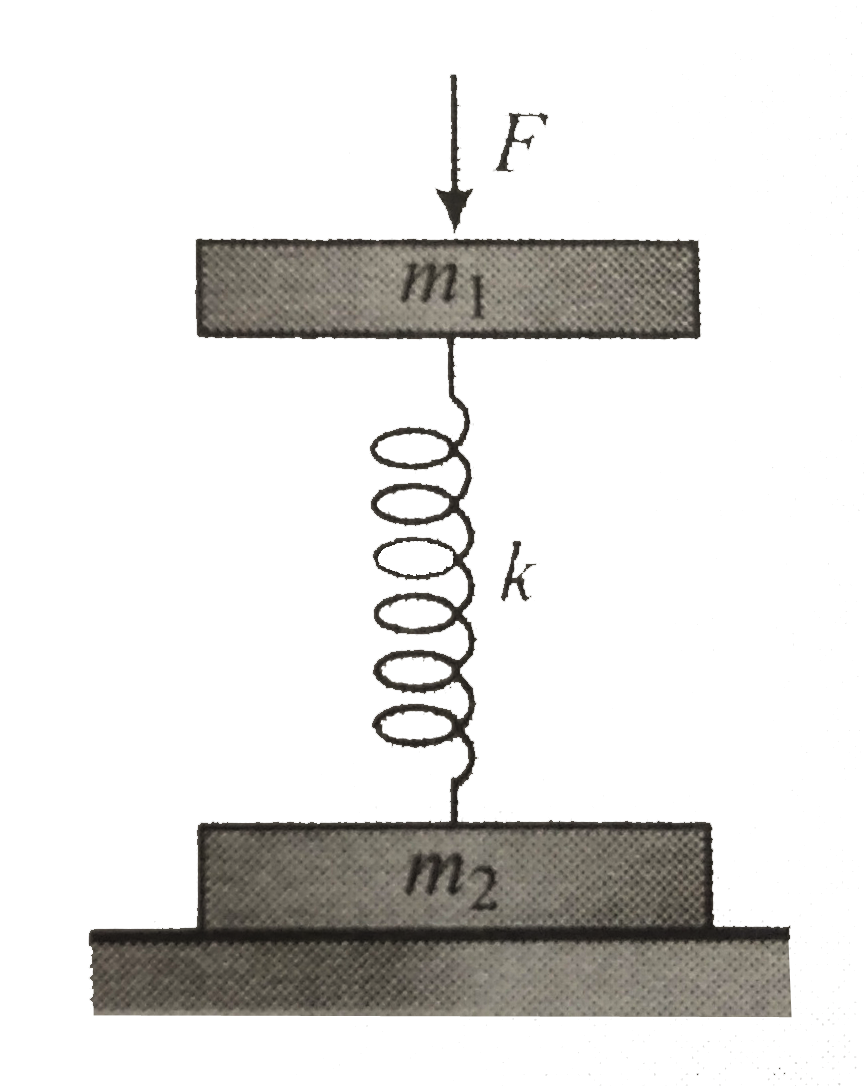
View SolutionA person lifts a parcel of mass 20 kg 1.5 m up from the ground and puts it in a truck. Find
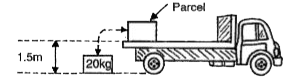
What force needs to be applied to the parcel to move it up at constant speed ?
View Solution
