The locus of the mid point of a chord of the circle x2+y2=4 which subtends a right angle at the origin is
A
x+y=2
B
x2+y2=1
C
x2+y2=2
D
x+y=1
Video Solution
Text Solution
The correct Answer is:C
As, we have to find the locus of mid-point of chord and we know that perpendicular from centre bisects the chord.
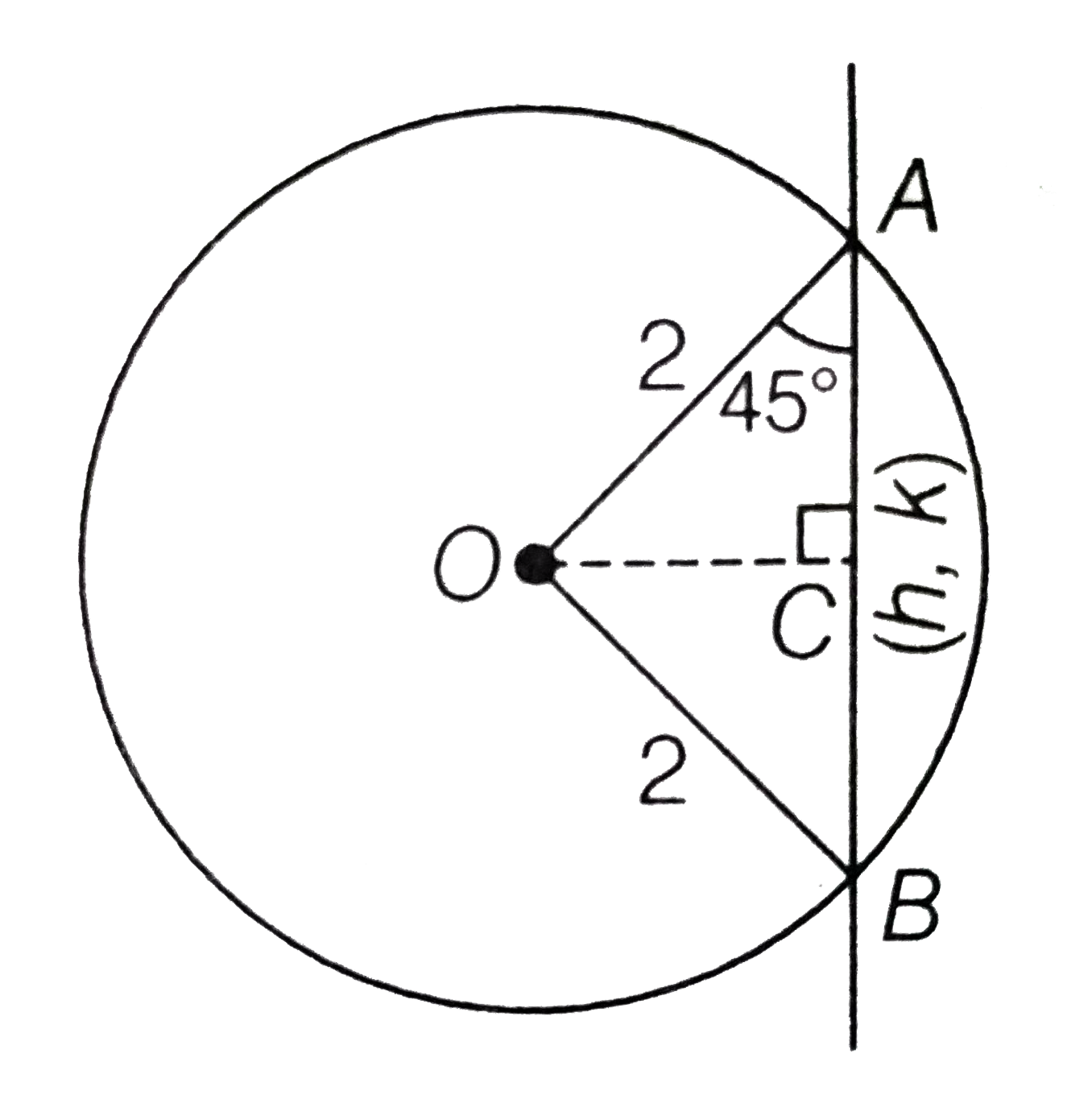
∴∠OAC=45∘ or OCOA=sin45∘
⇒OC=2√2
∴√h2+k2=OC
or x2+y2=2 is required equation of locus of mid-point of chord subtending right angle at centre.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The locus of the midpoint of chord of the circle x2+y2=1 which subtends a right angle at the origin is
Ax2+y2=14Bx2+y2=12Cxy=0Dx2−y2=0 - Question 2 - Select One
The locus of the mid -point of the chords of a circle x2+y2=4 ,which subtends a right angle at the centre , is
Ax+y=2Bx2+y2=1Cx2+y2=2Dx−y=0
The locus of the mid-points of a chord of the circle x2+y2=4 which subtends a right angle at the origin is
View SolutionThe locus of the midpoint of the chord of the circle x2+y2=4 which subtends a right angle at the origin is?
View SolutionThe locus of the midpoint of a chord of the circle x2+y2=4 which subtends a right angle at the origins is x+y=2 (b) x2+y2=1 x2+y2=2 (d) x+y=1
View SolutionThe locus of the mid points of a chord the circle x2+y2=18 which subtends right angle at the origin is
View SolutionThe locus of the mid-point of the chords of the circle x2+y2=4 which subtends a right angle at the origin is x+y=2 2. x2+y2=1 x2+y2=2 x+y=1
View SolutionFind the locus of the midpoint of the chords of the circle x2+y2=a2 which subtend a right angle at the point (c,0).
View Solution

