A solution of two liquids boils at a temperature more than the boiling point of either of them. Hence, the binary solution shows
negative deviation from raoult's law
positive deviation from raoult's law
no deviation from raoult's law
positive or negative deviation from raoult's law depending upon the composition.
The correct Answer is:A
The vapour pressure of the solution is lower than that of either of two liquids. Hence, the solution shows negative deviation from raoult's law.
Topper's Solved these Questions
Similar Questions
An aqueous solution containing urea found to have boiling point more than the normal boiling point of water (373.13 K). When the same solution was cooled, it was found that its freezing point is less than the normal freezing point of watre (273.13K). Explain there observations.
View SolutionAn aqueous solution containing urea was found to have boiling point more than the normal boiling point of water (373.13 K). When the same solution was cooled it was found that its freezing point is less than the normal freezing point of water (273.13 K). Explain these observations.
View Solution
Knowledge Check
Read the passage given below and answer the following questions :
Raoult's law states that for a solution of volatile liquids, the partial vapour pressure of each component of the solution is directly proportional to its mole fraction present in solution. Dalton's law of partial pressure states that the total pressure Ptotal over the solution phase in the container will be the sum of the partial pressures of the components of the solution and is given as:
Ptotal= P1+ P2
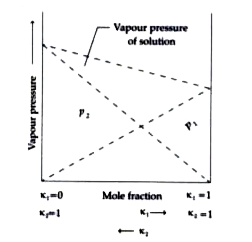
A solution of two liquids boils at a temperature more than the boiling point of either of them. What type of deviation will be shown by the solution formed in terms of Raoult' s law ?ANegative deviationBPositive deviationCFirst positive then negativeDFirst negative then positiveTwo liquids are mixed together to from a mixture which boils at same temperature and their boiling point is higher than the boiling point of either of them so they shows .
Ano deviation from Raoult's lawBpositive deviation from Raoult's lawCNegative deviation from Raoult's lawDpositive and negative deviation from Raoult's law depends upon the compositionAn azeotropic solution of two liquids has a boiling point lower than either of them when it:
Ashows negative deviation from Raoult's lawBshows no deviation from Raolut's lawCshows psoitive deviation from Raoult's lawDis saturated
A: An azeotropic solution of two liquids has boiling point lower than either of them.
R: Solution shows +ve deviation from ideal behaviour.
View SolutionWhen two liquids A and B are mixed, their boiling points become greater than both of them. The mixture is :
View SolutionAn azeotropic solution of two liquids has a boiling point higher than either of the two when it
View SolutionAn azeotropic solution of two liquid has boiling point lower than either of them when it
View SolutionAn azeotropic binary liquid mixture has boiling point lower than either of them when it:
View Solution

