Consider an infinite geometric series with first term a and common ratio r. if the sum is 4 and the sencond term is 3/4 ,then
a=23 , r=38
a=47,r=37
a=32,r=12
a=3,r=14
The correct Answer is:D
Sum of infinite geometric series,
S∞=a1−r
⇒4=a1−r⇒a=4−4r …(i)
Also T2=ar⇒ar=34 ….(ii)
From Eqs. (i) and (ii) , we get
a=4−4(34a)
a=4−3a
⇒a2−4a+3=0
⇒a2−3a−a+3=0
⇒a(a−3)−1(a−3)=0
⇒a=1,3
On putting a=3 in Eq. (ii) ,we get
3r=34
⇒r=14
Topper's Solved these Questions
Similar Questions
Consider an infinite geometric series with first term a and common ratio r. If its sum is 4 and the second term is 3/4, then a=47,r=37 b. a=2,r=38 c. a=32,r=12 d. a=3,r=14
View Solutionconsider an infinite geometric series with first term a and comman ratio r if the sum is 4 and the second term is 34 then find a&r
View Solution
Knowledge Check
Consider an infinite geometric series with first term a and common ratio r. if the sum is 4 and the sencond term is 3/4 ,then
Aa=74,r=37Ba=2,r=38Ca=32,r=12Da=3,r=14In a geometric progression with first term a and common ratio r, what is the arithmetic mean of first five terms?
Aa+2rBar2Ca(r5−1)/(r−1)Da(r5−1)/[5(r−1)]In a geometric series , the first term is a and common ratio is r. If Sn denotes the sum of the n terms and Un=Σnn=1Sn , then rSn+(1−r)Un equals
A0BnCnaDnar
Consider the infinite geometric series with first term a and common ratio r If its sum is '4' and second term is 34 then Sum of 10 terms of the series is
View SolutionLet G Let G be the sum of infinite geometric series whose first term is sinθ and common ratio is cosθ, while G' be the sum of a different infinite geometric series whose first term cosθ and common ratio is sinθ. Find the number of solutions of the equation, G=G' in [0,2π] is
View SolutionThe sum of an infinite geometric series is 6. If its first terms is 2, find its common ratio.
View SolutionLet sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
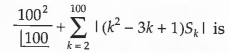 is
is
View SolutionThe sum of an infinite geometric series is 15 and the sum of the squares of these terms is 45. Find the series.
View Solution

