समीकरण x+|y|=2y पर विचार कीजिए । निम्नलिखित कथनों में से कौन-से कथन सही नहीं हैं ?
I.y,x के फलन के रूप में, सभी वास्तविक x के लिए परिभाषित नहीं है ।
II.y,x के फलन के रूप में x=0 पर सतत नहीं है ।
III.y,x के फलन में रूप में सभी x के लिए अवकलनीय है ।
नीचे दिए गए कूट का प्रयोग कर सही उत्तर चुनिए ।
I और II
II और III
I और III
I, II और III
The correct Answer is:D
दिया है,
x+|y|=2y
x+y=2y, जब y>0
⇒y=x
तथा x−y=2y, जब y<0
⇒y=13x
x+|y|=2y का आरेख
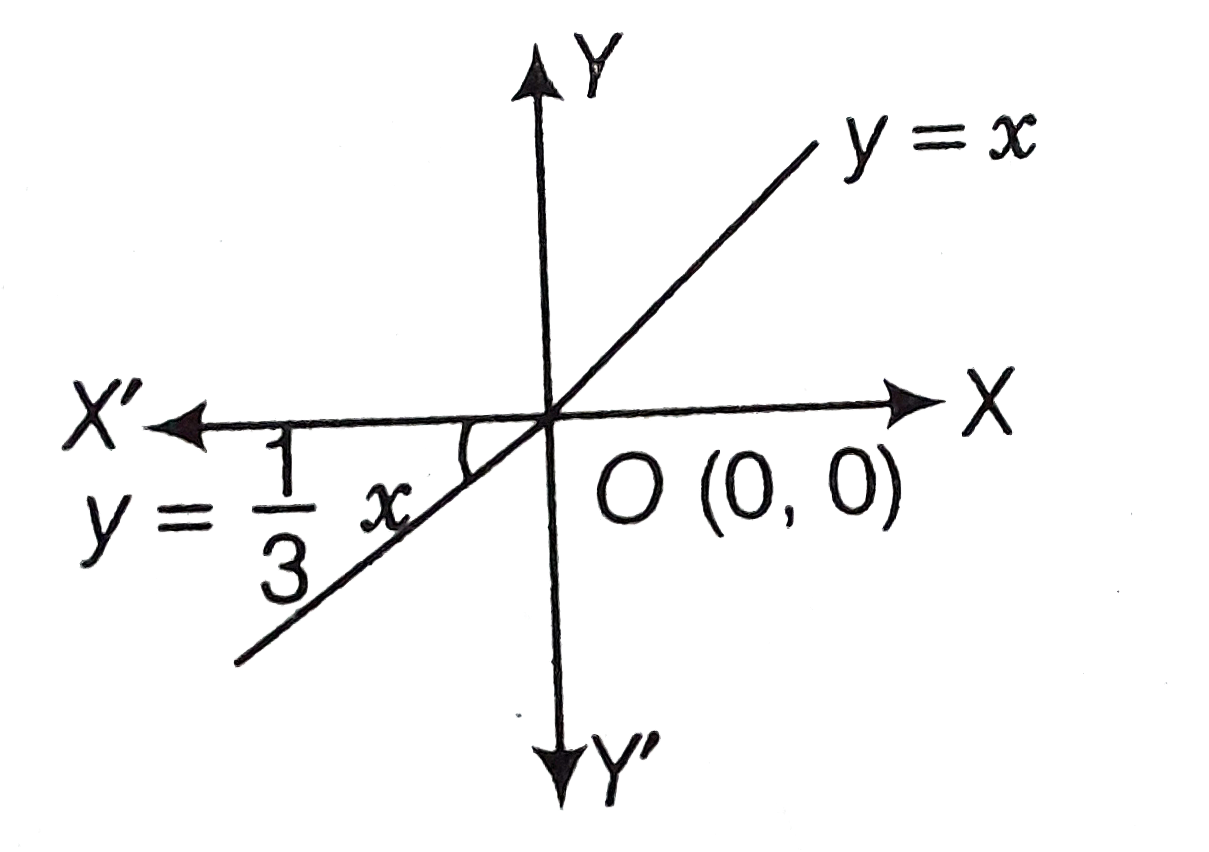
आरेख से,
y,x के फलन के रूप में, सभी वास्तविक x के लिए परिभाषित है ।
y,x के फलन के रूप में x=0 पर सतत है ।
तथा y,x के फलन के रूप में, x=0 के लिए अवकलनीय नहीं है ।
इस प्रकार, कथनI तथा III सही नहीं हैं ।
Topper's Solved these Questions
Similar Questions
यदि limx→0kxcosecx=limx→0xcoseckx है, तो k का मान है
View Solution∣∣ ∣ ∣∣−a2abacab−b2bcacbc−c2∣∣ ∣ ∣∣ किसके बराबर है ?
View Solutionभौतिक अधिशोषण के बारे में निम्नलिखित में से कौन सा कथन सही नहीं है?
View Solutionप्रकाश रासायनिक धूम के संबंध में निम्नलिखित में से कौन सा कथन सही नहीं है?
View Solutionफिनॉल फार्मेल्डिहाइड रेजिन के संबंध में निम्नलिखित में से कौन-सा कथन सही नहीं है ?
View Solutionएंजाइम उत्प्रेरण के लिए निम्नलिखित में से कौन सा कथन सही नहीं है?
View Solutionहाइड्राइडो के संबंध में निम्नलिखित में से कौन सा कथन सही नहीं है?
View Solutionतापसुघट्य बहुलकों के लिए निम्नलिखित में से कौन सा कथन सही नहीं है?
View Solutionषट्कोणीय निविड संकुलन के संबंध में निम्नलिखित में से कौन सा कथन सही नहीं है?
View Solutionअणु कक्षक सिद्धांत के संबंध में निम्नलिखित में से कौन सा कथन सही नहीं है?
View Solutionहीरे और ग्रेफाइट के संबंध में निम्नलिखित में से कौन सा कथन सही नहीं है?
View Solutionनिम्नलिखित में से कौन सा कथन (+) लैक्टोज के संबंध में सही नहीं है?
View Solutionउत्कृष्ट गैसों के बारे में निम्नलिखित में से कौन सा कथन सही नहीं है?
View SolutionRNA के संबंध में निम्नलिखित में से कौन सा कथन सही नहीं है?
View Solutionनिम्नलिखित में से कौन सा अणु एक संकलन बहुलक के लिए एकलक के रूप में कार्य नहीं कर सकता है?
View Solutionनिम्नलिखित में से कौन सा कथन B और AI दोनों के लिए सही नहीं है?
View Solution