यदि
f(x)=⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩sin(a+1)x+2sinxx,x<02,x=0√1+bx−1x,x>0
x=0 पर सतत है, तब a व b के मान ज्ञात कीजिये |
दिया है,
f(x)=⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩sin(a+1)x+2sinxx,x<02,x=0√1+bx−1x,x>0
दिया है कि फलन f(x),x=0 पर सतत है |
∴ (बायाँ पक्ष ) x=0 = ( दायाँ पक्ष) x=0 = f(0) ...(1)
अब, बायाँ पक्ष = limx→0−f(x)
=limh→0f(0−h)
[x=0−h रखने पर, जब x→0 , तब h→0]
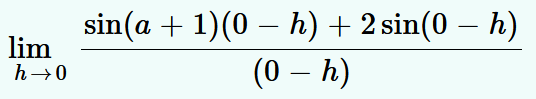
=limh→0−sin(a+1)h−2sinh−h
[∵sin(−θ)=−sinθ]
=limh→0sin(a+1)h+2sinhh
=limh→0sin(a+1)hh+limh→02sinhh
=limh→0sin(a+1)h(a+1)h×(a+1)+2limh→0sinhh
=1×(a+1)+2×1
[∵limx→0sinxx=1]
=a+1+2=a+3
तथा दायाँ पक्ष =limx→0+f(x)
=limh→0f(0+h)
[x=0+h रखने पर, यदि x→0 तब h→0]
=limh→0√1+b(0+h)−10+h
=limh→0√1+bh−1h
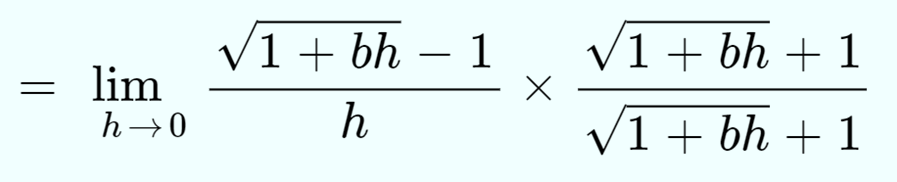
[अंश व हर में √1+bh+1 से गुणा करने पर ]
=limh→0(1+bh)−1h(√1+bh+1)
=limh→0bhh√1+bh+1
=limh→0b(√1+bh+1)=b√1+0+1=b2
समीकरण (1 ) से,
a+3=b2=2
⇒a+3=2 तथा b2=2
⇒a=−1 तथा b=4
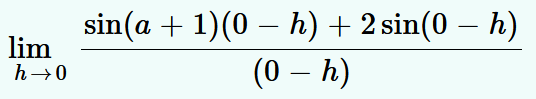
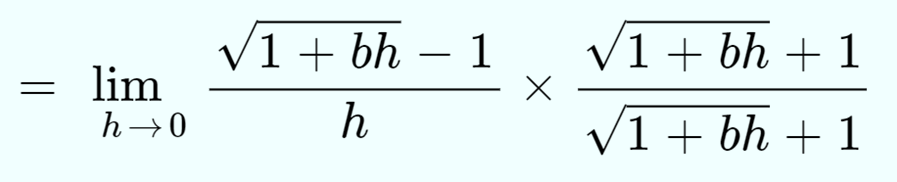
Topper's Solved these Questions
- सांतत्यता BOOK - BALAJI PUBLICATIONCHAPTER - सांतत्यता EXERCISE - अभ्यास प्रश्न 6.1
22 Videos
- सांतत्यता BOOK - BALAJI PUBLICATIONCHAPTER - सांतत्यता EXERCISE - अभ्यास प्रश्न 6.2
16 Videos
- समाकलन क्रमशः BOOK - BALAJI PUBLICATIONCHAPTER - समाकलन क्रमशः EXERCISE - स्वमूल्यांकन परीक्षण
20 Videos
- सारणिक BOOK - BALAJI PUBLICATIONCHAPTER - सारणिक EXERCISE - स्वमूल्यांकन परीक्षण
27 Videos
Similar Questions
फलन f(x) निम्नवत परिभाषित है -
f(x)=1 यदि x>0
=−1 यदि x<0
=0 यदि x=0
सिद्ध कीजिये कि limx→0f(x) अस्तित्व में नहीं है |
View Solutionसिद्ध कीजिये कि फलन f(x)={x,x≥01,x<0, बिंदु x =0 पर सतत नहीं है |
View Solution1x2−9
View Solutionसिद्ध कीजिए कि ∣∣ ∣ ∣∣0sinα−cosα−sinα0sinβcosα−sinβ0∣∣ ∣ ∣∣=0
View SolutionIf the function f as defined below is continuous at x=0find the values of a,b and c f(x) = {(sin (a+1)x +sin x)/x, x<0 and c, x=0, and (sqrt(x+bx^2)-sqrt(x))/(bx^(3/2)), x>0
View Solutionयदि फलन f(x)=⎧⎨⎩(4x−1)3sin(x/4)log(1+x2/3)x≠0kx=0, x=0, पर सतत है तब k=
View SolutionIf f(x)={xmsin(1x)x≠00x=0 and f(x) is continuous at point x=0 ,then
View Solutionसिद्ध कीजिए की फलन
f(x)={x2sin1x यदि x≠00 यदि x=0
बिंदु x=0 पर अवकलनीय नहीं है।
View Solutionf(x)={sin1xx≠01x=0 पर संतत है अथवा असंतत ।
View Solutionयदि प्रदत फलन बिन्दु x = 0 पर संतत हो, तो a, b व c के मान ज्ञात कीजिए -
f(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩sin(a+1)x+sinxx,यदिx<0 c,यदिx=0√x+bx2−√xbx3/2,यदिx>0
View SolutionIf f(x) is continuous at x=0, where f(x)=⎧⎨⎩sinxx+cosx, for x>04(1−√1−x)x, for x<0, then f(0)=
View SolutionIf f(x) {1for −π2<x<01+sinxfor0≤x<π2,then at x= 0 ,f'(x) -
View SolutionIf f(x) is continuous at x=0, where f(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩sin(a+1)x+sinxx, for x<0c, for x=0√x+bx2−√xb√x, for x>0, then
View SolutionA function f is defined by
f(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩sin(a+1)x+sinxx if x<0c if x=0(x+bx2)12−x12bx32 if x>0
It f(x) is continuous at x = 0 , find the values of a,b and c .
View Solutionনিম্নে সংঞ্জাত, f(x) অপেক্ষক x=0 বিন্দুতে সন্তত, a,b ও এর মান নির্ণয় করো:
f(x)={sin(a+1)x+sinxx যদি x<0 হয়
c যদি x=0 হয়
√x+bx2−√xbx32 যদি x>0 হয়
View Solution
