In Figure, if P is (2, 4, 5), find the coordinates of F.
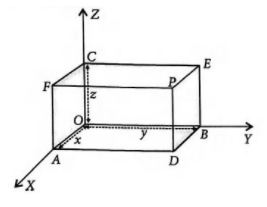
Given ,
p(2,4,3)
So, x=2,y=4,z=5
Point F lies in XZ plane.
So, its y coordinate will be zero.
then Co ordinate of F=(x,0,z)
=(2,0,5)
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - MISCELLANEOUS EXERCISE6videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
- BOOK - NCERTCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE 12.14videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
- BOOK - NCERTCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE 12.25videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
- BOOK - NCERTCHAPTER - CONIC SECTIONSEXERCISE - EXERCISE 11.115videos
CONIC SECTIONS
- BOOK - NCERTCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EXERCISE 13.38videos
LIMITS AND DERIVATIVES
Similar Questions
Knowledge Check
- Question 1 - Select One
In the following figure, if the coordinates of P are (a,b,c) then the coordinates of A,B and C are respectively
A(a,0,0),(b,0,0),(c,0,0)B(a,0,0),(0,b,0),(0,0,c)C(0,0,a),(0,b,0),(c,0,0)D(a,b,c),(b,c,a),(c,a,b)
The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2,−5)andR(−3,6), then find the coordinates of P.
View SolutionIf P(-2,-5) and Q(4,3) and point R divides the segment PQ is
the ratio 3:4 then find the coordinates of points R.View SolutionA line intersects the y-axis and x-axis at the points P and Q respectively. If (2, 5) is the mid-point of PQ, then find the coordinates of P and Q.
View SolutionThe x-coordinate of a point P is twice its y-coordinate. If P equisdtant from Q(2,−5)andR(3,6) find the coordinates of P .
View SolutionIf the origin is shifted to the point (2,3) the coordinates of a point become (5,-4). Find the original coordinates, which the axes are parallel.
View SolutionLet P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
View SolutionIf the coordinates of points A and B are (-2, -2) and (2, -4) respectively, find the coordinates of the point P such that AP=37AB, where P lies on the line segment AB.
View Solution
