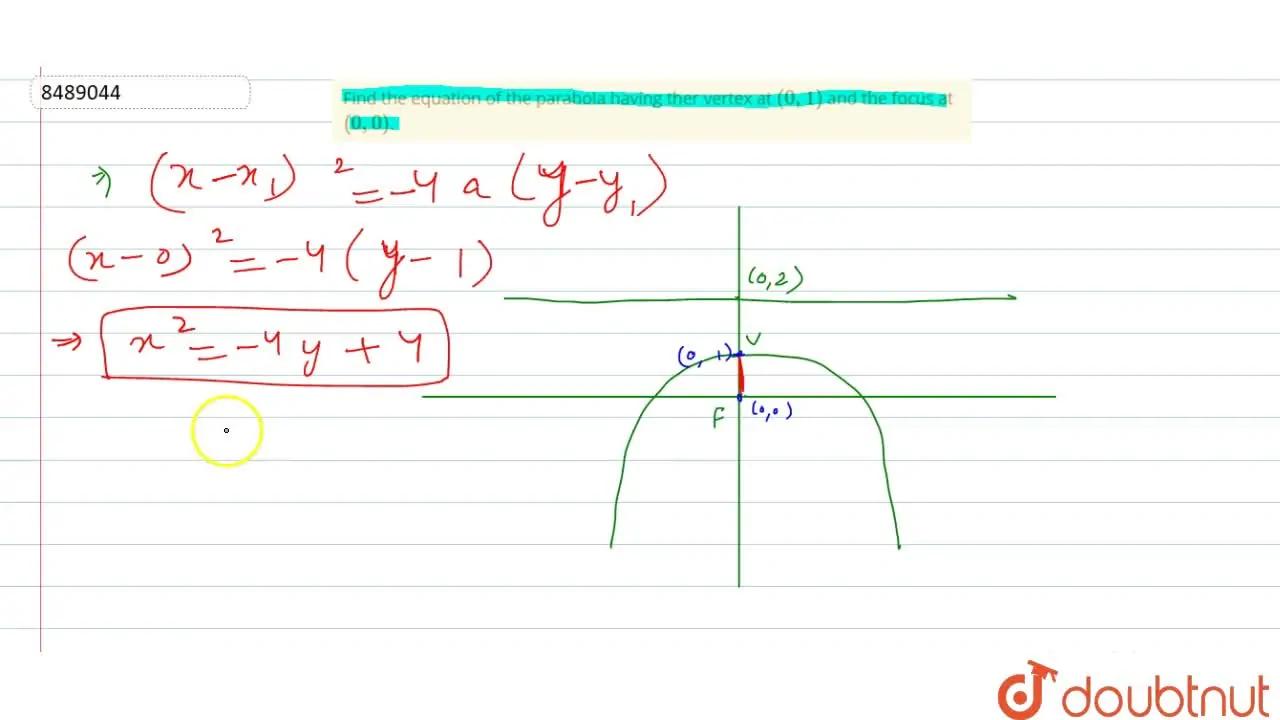
Find the equation of the parabola having ther vertex at (0,1) and the focus at (0,0).
Step by step video & image solution for Find the equation of the parabola having ther vertex at (0, 1) and the focus at (0, 0). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Find the equation of the parabola having vertex at (0, 0) and focus at (−2,0).
View SolutionFind the equation of a parabola having its vertex at A(1,0) and focus at S(3,0).
View SolutionFind the equation of the parabola with vertex at (0, 0) and focus at (0, 2).
View SolutionFind the equation of the parabola with vertex at (0, 0) and focus at (0, 5).
View SolutionThe equation of the parabola with vertex at (0, 0) and focus at (0, 4) is
View SolutionFind the equation of the parabola with vertex (0,0) and focus (3,0).
View SolutionFind the equation of the parabola with vertex at (0,0) and focus at (0,2) Also, find the equation of its directrix.
View SolutionFind the equation of the parabola with vertex at the origin and focus at F(-2, 0).
View SolutionFind the equation of parabola
(i) having its vertex at A(1,0) and focus at S(3,0)
(ii) having its focus at S(2,5) and one of the extremities of latus rectum is A (4,5)View SolutionFind the equation of parabola
(i) having its vertex at A(1,0) and focus at S(3,0)
(ii) having its focus at S(2,5) and one of the extremities of latus rectum is A (4,5)View Solution